
1. ���w����
�@���q���m�̌����Ƃ��ẮA���L�����A�C�I�������A������������\�I�Ȃ��̂ƂȂ�܂��B
�����͑S�ăN�[�����͂��琶������̂ł����A���q�̓d�q��Ԃ�G�l���M�[��ԂȂǂ���A�����̏��ς��Ă��邱�ƂɂȂ�܂��B
2. ���L����
�@���L�����́A�������q�̂悤�ɓd�דI�ɒ����̂��̓��m���������錻�ۂ̂��Ƃ������܂��B
���̗��R�́A�d�דI�ɒ����ł������Ƃ��Ă��A���q���m���\���ɋ߂Â��Ȃ�A�d�q�̕��d�ׂƌ��q�j�̐��d�ׂɂ��A���������悤�ɂȂ邽�߂ł��B
�@���L�����́A�o���̌��q�ԂɌ����O�������݂��A����ɓd�q���[�U���ĖO�a���邱�Ƃɂ��܂��B
���̖O�a�́A�p�E���̔r�������ɂ��܂��B
�܂�A����O���ɂ�2�܂ł����d�q�����邱�Ƃ��ł��Ȃ��Ƃ������Ƃɂ���āA�d�q�̏[�U�͐�������邱�ƂɂȂ�܂��B
���̌����O���͕��q�O���i�����̌��q�j�𒆐S�Ƃ���O���j�ƂȂ�܂����A����͌��q�O���������G�ɂȂ邽�߁A���ʂɂ͌��q�O���̏d�Ȃ�ɂ���čl���邱�ƂɂȂ�܂��B
����͌��q�������@�ƌĂ����̂ł��B
�@���q�������@�Ƃ��čl�����ꍇ�A���L�����͕��ʂQ�̌��q�ɂ�錋���Ƃ��čl���邱�Ƃ��ł��܂��B
���̂��Ƃ́A���q�Ԃɂ����ēd�_�̖��x�������Ȃ�A�����������邱�Ƃɂ��܂��B
�܂�A���q�j���m�͎��̂悤�Ɍ������邱�ƂɂȂ�܂��B
�@���ɁA���q�ԍ����傫�����f�i�������A�n���Q�����f�Ɗ�K�X���f�͏����܂��j��A�k���`�����ꂽ����̃A���J���������f�Ȃǂł́A�d�q����o���₷���Ȃ�܂��B
�d�q����o�������q�͗z�C�I���ƂȂ�A����͓d�q������ĉA�C�I���ƂȂ������q�ƃC�I���������s�Ȃ��悤�ɂȂ�܂��B
�������A���̂悤�ɗL�ɐ��̗n�}�̒��ł́A�z�C�I���Ƃ��Ă����݂���悤�ɂȂ�܂��B
�܂��A�d�q���������ɕ��o���ꂽ�ꍇ�́A�V���d�q�ƂȂ��ċ����������R�ɔ�щ�邱�ƂɂȂ�A����͊e���q���C�I�������̂悤�Ɍ��������邱�ƂɂȂ�܂��B
���̌����̂��Ƃ́A���������ƌĂ�܂��B
�@���L��������{�I�ɂ̓N�[�����͂ɂ����̂ŁA���q�̓d�q�������Ԃɂ�葽���Ǎ݂��āA�o���̌��q�j�������̓d�q�ƈ����������ƂɂȂ�܂��B
�������Ȃ���A���q�̓d�q�͎��R�ɕ��z�ł���킯�ł͂Ȃ��āA���q�O���܂��͕��q�O���ƌĂ����̂ɔz�u���邱�ƂɂȂ�܂��B
�@�������A���̂��߂ɂ͌��q�j�̐��d�ׂ̉e�����y�Ԕ͈͂ɓd�q�����݂ł��邱�Ƃ������ƂȂ�܂��B
����́A���q�ɂ����ĕk���ł��Ă��Ȃ����Ƃ������ƂȂ�܂��B
�����k���ł��Ă���ꍇ�ɂ́A���̊k�ɂ���Č��q�j�̐��d�ׂ��u�Օ��v����Ă��܂��܂��B
�@���L�������s���悤�Ȍ��q�́A���3�����܂ł̌��f���L�f(Br)�A���E�f(I)�Ƃ������n���Q�����f�ɂȂ�܂��B
�������A�k���`������Ă���w���E���Ȃǂ̊�K�X���f�͏����܂��B
|
[���q�jA] �c [�d�_�̏d�Ȃ�] �c�@[���q�jB] |
�@�d�_�́A���q�j�Ԃɂ̂ݑ��݂��Ă���킯�ł͂Ȃ��A�o���̌��q�j���ӂɂ����݂��Ă��܂��B �����A���̒��ԕ����ł̓d�ז��x���������Ƃ���A���q���m�̌����ɑ傢�Ɋ�^������̂ƂȂ�܂��B �܂�A���q�j���m�̐˗͂����̒��ԕ����ɑ��݂���d�q�_���u���a�v���āA�o���̌��q�j���������邱�ƂɂȂ�܂��B ���̂��Ƃ́A�N�[�����͂������̓��ɔ���Ⴕ�Ďキ�Ȃ邱�Ƃ��W���Ă��܂��B �܂�A���葤�̌��q�j�ɂ��˗͂̑傫���͒��Ԃɂ���d�q�̈��͂���1/4�{�ƂȂ邱�Ƃɂ��܂��B �����Ǎݓd�q������̑��ɂقƂ�NJ��Ȃ�A�d�q�ɂ��Օ�����A�����͎キ�Ȃ�A�����͋��L�����I�ł͂Ȃ��Ȃ�܂��B
�@���q��
�@���L�����̏ꍇ�A�����ɖO�a�������邱�Ƃ���A���錳�f�̌��q�����̌��f�̌��q�Ɗ�����ł��邩�Ƃ������Ƃɂ͌��E������A���̔\�͂�\�킷�p��Ƃ��Č��q��������܂��B
����͌��q���m���݂��̕s�Γd�q�ɂ���Č�������Ƃ����l�������ɂ������̂ŁA����Ԃł̕s�Γd�q������\�ȕs�Γd�q�������q���ƂȂ�܂��B
�@�Ⴆ�A���f��1���A�_�f��2���A���f��3���A�Y�f��4���ɂȂ�܂��B
�����̌��f��2�����܂ł̌��f�ŁA��ʓI�����ɂ����Ă͓d�q��L�k�Ɏ��܂邱�Ƃ���A�����\�ȕs�Γd�q���ɂ͖��m�Ȍ��E������܂��B
�܂�A���f����t�b�f�܂ł͊���Ԃł̕s�Γd�q�������q���ƂȂ�A�x�����E������Y�f�܂ł͗�N��Ԃł̕s�Γd�q�������q���ƂȂ�܂��B
�@�������A3�����ȍ~�ɂȂ�ƁA��ʂ̃G�l���M�[���ʂւ̑J�ځi3p�O������3d�O���ւ̑J�ڂȂǁj����r�I�e�ՂɂȂ邱�Ƃ���A�����\�ȕs�Γd�q���͖��m�ɂ͒�܂�܂���B
�Ⴆ�A�C�I�E�͎_�f�Ɠ������̌��f�Ȃ̂ŁA�ʏ��2���ƂȂ�܂����A��������ł�3�`6���ɂȂ邱�Ƃ��ł��܂��B
���̂悤�Ɍ��q���ʼn��w�������l����ꍇ�ɂ́A���f�̎����\�Ō��f���������ڂ̂��̂ł��邩��F�����Ă����K�v������܂��B
�@�������Ȃ���A���w�����͕s�Γd�q���m�̋��L�����łȂ��A����̔L�d�q�̋��L�ł���z�ʌ����̏ꍇ������܂��B �Ⴆ�AH3O+�ł́A��͔L�d�q�ɂ���Đ��f�ƌ������Ă��āA���̏ꍇ�̎_�f�̌��q����3�ɂȂ�܂��B
�@�_����
�@���q���Ǝ����悤�ȊT�O�̂��̂Ɏ_����������܂����A����͎_���Ҍ��������l����ۂɖ𗧂��̂ƂȂ�܂��B
�_�����́A�d�q�̈ړ��̗e�Ղ��ɂ���āA���������̈�̌��f���瑼���̌��f�ɉ��z�I�Ɋ��S�Ɉړ��������Ƃ��̌��f�̓d�א��ɂ���ĕ\�킳�����̂ł��B
�Ⴆ�AH2O�ł́A�_�f�̕����A�����f�ł��邱�Ƃ���A�d�q�͎_�f���Ɉړ����邱�ƂɂȂ�A�_�f�̎_������-2�ƂȂ�܂��B
���̏ꍇ�A�_�f�̎_�����̐�Βl�͌��q���Ɠ������Ȃ�܂��B
�@�������A����̌��f���m���������Ă���ꍇ�ɂ́A�d�q�̈ړ��͂Ȃ����ƂɂȂ�܂��B
���̂悤�ȏꍇ�ɂ́A�_�����̐�Βl�͌��q���Ƃ͓����ɂȂ�܂���B
�Ⴆ�ANH2-NH2�̏ꍇ�̒��f�̎_������-2�ƂȂ�܂��B
�@�܂��ANH4�̂悤�ɁA����z�ʌ������Ă���ꍇ�ɂ͂��̐��f�Ƃ̓d�q�̈ړ��͂Ȃ����Ƃ���i���̋��L�d�q�͒��f�̂��̂ł��������߁j�A���̎_������-3�ƂȂ�܂����A���̌��q����4�ł���A�_�����̐�Βl�͌��q���Ɠ����ɂ͂Ȃ�܂���B
�@�_���������傷�邱�Ƃ́A���d�ׂ�������Ƃ������Ƃł���A����͓d�q���D���邱�Ƃ��Ӗ����Ă��܂��B ������_���Ƃ����̂́A�_�f�͑�\�I�ȉA�����f�ł���i������A���̋������̂Ƀt�b�f������܂����A����͎_�f���q�̂悤�Ɉ�ʓI�ł͂���܂���j�A����Ƃ̌����͓d�q���_�f���Ɉړ����₷�����Ƃɂ��܂��B ����A�Ҍ��̕��͎_�������������邱�Ƃł���A����͒D��ꂽ�d�q�����ɖ߂�Ƃ������Ƃł�����A�Ҍ����ꂽ�Ƃ������ƂɂȂ�܂��B �Ȃ��A�_���Ҍ������ł́A�d�q��^���鑤�̂��̂͊Ҍ��܂ƌĂ�A�d�q����鑤�i�Ƃ������͓d�q��D�����j�̂��͎̂_���܂ƌĂ�܂��B
2.1 �����̎d��
�@�������q���m�̌����̎d���Ƃ��ẮA�o���̌��q�̕s�Γd�q���m�ɂ�錋���ƁA����̌��q�ɂ��L�d�q�ɂ�錋��������܂��B
�@�s�Γd�q���m�ɂ�錋��
�@���q�j�ԂɋǍ݂���d�q�́A�ʏ�͂Q�̌��q�̕s�Γd�q�i���q�O���Ɉ�����������Ă�����́j�����ꂼ����������̂ɂȂ�܂��B
���̂��Ƃ́A�ȉ��̂悤�ɍl���邱�Ƃ��ł��܂��B
�@�����̌��q�̏�ԂƂ��ẮA����G�l���M�[���ʂ̋O�����O�a���đΓd�q�݂̂ɂ���Č`������Ă�����̂ƁA���̋O�������O�a�ŕs�Γd�q��������̂ɕ�����܂��B
�i���̂��Ƃ́A�G�l���M�[���ʂ̓������O������������Ȃ�A�d�q���m�̐˗͂ɂ��A�Ă���O������[�U���邱�Ƃɂ��܂��B�j
�@�Ȃ��A�s�Γd�q���Q�̌��q�ŋ��L����Ƃ����ꍇ�A�d�C�A���x�̈Ⴂ�ɂ��A�d�_�͓d�C�A���x�̍������Ɉ�����邱�ƂɂȂ�܂��B
�������L�d�q�������ɂ�������ڂ����ꍇ�ɂ́A���L�d�q����������͉A�C�I���ƂȂ�A�����D��ꂽ���͗z�C�I���ƂȂ�܂��B
�����āA�����͋��L�����ł͂Ȃ��A�C�I�����������邱�ƂɂȂ�܂��B
�C�I���ƂȂ����ꍇ�ɂ́A�����I�ɃN�[�����͂������Č������邱�ƂɂȂ�܂�����A�����̗��C�I���́A���݂ɋ�Ԃ��[�U���邱�ƂɂȂ�܂��B
�@�L�d�q�ɂ�錋��
�@�s�Γd�q�������̂ł��A���̌��q�Ƌ��L�������Ă��āA���R�ȕs�Γd�q���Ȃ��Ƃ����ꍇ������܂��B
���̏ꍇ�ɂ́A�����̑Γd�q���Ă���O���ɂ����������Č������邱�Ƃ��ł��܂��B
��������L�����̈��ł����A����͒ʏ�̋��L�����Ƃ͈قȂ邱�Ƃ��A�z�ʌ����i�h�i�[�E�A�Z�v�^�[�����j�ƌĂ�܂��B
�@�����G�l���M�[
���L�������������Ƃ��ɂ͌����G�l���M�[�������܂����A����͂��̌������𗣂�����G�l���M�[�ɂقړ������Ȃ�܂��B
�قړ������Ƃ����̂́A�q���q�̏ꍇ�ɂ͓������Ȃ�̂ł��A�����q���q�̏ꍇ�ɂ͓������Ȃ�Ȃ����Ƃ����邩��ł��B
2.2 ���W�J��
�@���W�J���Ƃ����̂́A�V����̂��Ƃł��B
�܂�A���q�̂ǂ����ŋ��L��������ĕ��A�s�Γd�q�i��d�q�Ƃ��j�����悤�ɂȂ������̂������܂��B
���ꂪ�P�݂̂̒������q�ƂȂ����ꍇ�ɂ́A���̌��q�Ƃ������ƂɂȂ�܂��B
�@���W�J���̂悤�ɕs�Γd�q�����ꍇ�A���̃��W�J���Ɨe�ՂɌ������邱�ƂɂȂ�܂��B
�܂��A���q�Ƃ��e�Ղɔ������₷���Ȃ�܂��B
���̂��Ƃ́A���q�Ƃ̔����ŁA���W�J���̕��͌�����������K�v���Ȃ����Ƃɂ��܂��B
���̂��߁A���W�J���͔��ɉ��w���������������̂ƂȂ�܂��B
2.3 �z�ʌ���
�@p�d�q��esp�����O���͕��������������Ƃ���A���q�͓d�q�k�����܂�܂ŁA�����̓d�q��ߊl���邱�Ƃ��ł��܂��B
���̂��Ƃ͓d�C�A���x�̍������f�ł͂悭�N����܂��B
�@�z�ʌ����ɂ���ĔL�d�q��^�������̓h�i�[���ƂȂ�A�������������̓A�N�Z�v�^�[���ƂȂ�܂��B
�h�i�[���͓d�q��^���Č��q���m�ŋ��L���邱�Ƃ��畉�d�ׂ��������A���d�ׂ�тт邱�ƂɂȂ�܂��B
�A�N�Z�v�^�[���́A�t�ɕ��d�ׂ�тт邱�ƂɂȂ�܂��B
�@���f
�@����͕s�Γd�q��3����A���̂��ꂼ�ꂪ���L���������Ă���Ƃ������Ƃ��A�L�d�q�Ȃǎ����Ȃ����ƍl���邩������܂��A�A�����j�ANH3�̂悤�ȏꍇ�ɂ́A���f�Ƃ̌����͍����O���ɂ���čs�Ȃ��Ă��āA1�L�d�q����i�Q���j�������Ă��܂�����A�����^���邱�Ƃɂ���Ĕz�ʌ������s�����Ƃ��ł��܂��B
�@�����O���ɂ͓d�q����܂œ��邱�Ƃ��ł��邱�Ƃ��A�o���ɕs�Γd�q������ꍇ�ɂ́A�����̓d�q�ɂ���ď[�U����܂��B
����ɕs�Γd�q������A�����ɂ͑Γd�q�݂̂����Ȃ��Ƃ����ꍇ�ɂ́A��҂̕��́A�Γd�q���āA��̕s�Γd�q�Ƃ��Ă���A�Γd�q���m�ɂ���Č������邱�ƂɂȂ�܂��B
�Γd�q���邽�߂ɂ́A�Γd�q�̈���Ă���O���ɏ��ʂ�����K�v�����邱�Ƃ���A�G�l���M�[���K�v�ɂȂ�܂����A����͌����G�l���M�[�ɂ���ĕ⏞����邱�ƂɂȂ�܂��B
�@���̑Γd�q�̕���ɂ���ĕs�Γd�q�������A���q���������邱�ƂɂȂ�܂��B
���̑�\�I�Ȃ��̂��Y�f�ŁA���̕���ɂ����sp3�����O���Ȃǂ̓d�q�������邱�ƂɂȂ�܂��B
�@�H����H�ׂăG�l���M�[��Ƃ������Ƃ́A���Ⴂ�G�l���M�[�i��苭��������Ԃ̂��Ɓj�̕��q�����ɕϊ�������A�Ƃ������Ƃ��Ӗ����Ă��܂��B
�܂�A�H�����g�ɃG�l���M�[���܂܂�Ă���킯�ł͂Ȃ��A���ꂩ��G�l���M�[���擾���邽�߂ɂ́A�������̕ϊ����K�v�ɂȂ�܂��B
�@���ɕs�Γd�q�������W�J���̏ꍇ�ɂ́A���L�������𗣂�����K�v���Ȃ��A�������\�ɂȂ邱�Ƃ���A��荂���G�l���M�[�̂��̂ƂȂ�܂��B
�@���L�������s���悤�Ȍ��q�́A�G�l���M�[�I�ɕs����ł��邽�߁A���̌��q�Ƌ��L�������s���A���艻���邱�ƂɂȂ�܂��B
���������āA�ʏ�A���̂悤�Ȍ��q�͕��q���`�����Ă��܂��B
�@�������A���ɂ͗�O�I�ɕ��q�̏�Ԃŕs�Γd�q�������̂�����A����Ƃ��Ă͎_�f���q����\�I�ł��B
�������͂�s�Γd�q�������Ƃ���A���W�J���Ƃ������ƂɂȂ�܂��B
����ȒY�����f���R�Ă���̂́A��C���ɖL�x�ɂ���_�f���q�Ƃ̔����ɂ��܂��B
�@�_�f���q�͎_�f���m����d�����������̂ƍl�������ł����A���ۂɂ͂��̂悤�ɂ͂Ȃ�܂���B
���̏�Ԃ͌��q�������@�ł͐����ł����A���q�O���@�ɂ���Đ�������܂��B
�����������q�͔�r�I�H�ŁA���ʃ��W�J���Ƃ����A�s�Γd�q�������q��A���q���������q�c�ɂȂ�܂��B
�@����Ɠ��l�ɁA���q�̎����Ă���p�d�q�Ȃǂ�ߊl���邱�Ƃ��ł��܂��B
�������A�Y�f�⒂�f�A�_�f�Ȃǂ̌��q�͈�ʂɋ��L�����������肵�Ă��܂�����A�ߊl�ΏۂƂȂ�d�q�͔L�d�q�ɂȂ�܂��B
���������āA��������ɂ́A��̋O�����Ă���K�v������܂��B
���̂悤�ɂ��Č��������ꍇ���A�s�Γd�q���m�ɂ�鋤�L�����̏ꍇ�Ɠ����ɂȂ�A��ʂ͂��܂���B
�@�Ⴆ�A���f���h�i�[���ɂȂ����ꍇ�A����͐��d�ׂ������ƂɂȂ�܂��B
���̂��Ƃ͒��f���s�Γd�q�ɂ���ċ��L�������Ă���ꍇ�Ƃ͋t�ɂȂ�A���̏ꍇ�̒��f�ɂ��Ă͔z�ʌ������l���Ȃ��ƍ������邱�ƂɂȂ�܂��B
�@�Ⴆ�A�A�����j�A�iNH3�j�Ɛ��f�C�I���iH+�j�����������A�����j�E���C�I���iNH4+�j������܂��B
����͎��̂悤�Ȍ����ƂȂ�܂��B
|
�@�_�f
�@����͈�̔L�d�q��2�̕s��p�d�q�������Ă��܂�����A���̕s��p�d�q�ɂ���Ă��ꂼ�ꋤ�L�������������A�L�d�q�ɂ���Ĕz�ʌ������s�����Ƃ��ł��܂��B
�܂��A�����O����Ԃ̂��̂�����A���̏ꍇ�ɂ͔L�d�q��2�i�Q���j�������Ă��܂�����A2�̔z�ʌ������s�����Ƃ��ł��܂��B
�@�Ⴆ�A�����q�Ɛ��f�C�I��H+�i�v���g���j����������OH3+������܂��B
����͎��̂悤�Ȍ����ƂȂ�܂��B
|
�@�܂��A��_���Y�f���z�ʌ������`���������̂ŁA����͓�d�����Ɣz�ʌ����ɂ��A���̂悤�ɎO�d�����������̂ɂȂ�܂��B
|
�@�Ȃ��A��_���Y�f�̏ꍇ�ɂ́A���̂悤�ɕs�Γd�q���m�ɂ���ē�d�����������̂ƂȂ�A���̕��q�̏ꍇ�ɂ͋ɐ�������܂���B
|
|

�@���L�����́A��ʂɑo���̌��q�O�����d�Ȃ�ꍇ�ɋN��܂��B
���̗��R�́A���̏d�Ȃ�ɂ����ēd�ז��x�������Ȃ邱�Ƃɂ��܂��B
���̂��Ƃ́A�ȉ��̐}�Ŏ������Ƃ��ł��܂��B
�@�܂��A���d�q�̏d�Ȃ肪�Ȃ��ꍇ�̑o����s�d�q�O�����d�˂����̂́A���̂悤�ɂȂ�܂��B
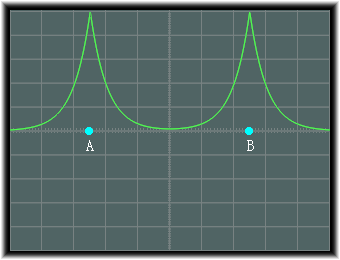
���̏ꍇ�ɂ́A�����q�j�ɂ����ēd�q�͋ϓ��ɕ��z����Ƃ������ƂɂȂ�A�ǂ���̌��q�j���ړ����Ȃ����ƂɂȂ�܂��B
�@���d�q�_���d�Ȃ邭�炢�ɋ߂Â����ꍇ�ɂ́A���̂悤�ɂȂ�܂��B�@
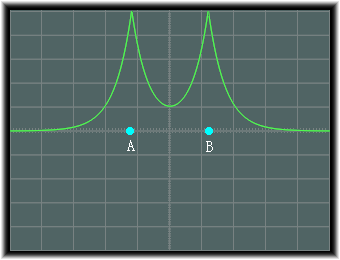
���̏ꍇ�ɂ́A���q�j�Ԃ̓d�ז��x�������Ȃ�A�ǂ���̌��q�j�������̌��q�j�̕��Ɉ������邱�ƂɂȂ�܂��B
�@�������A�߂Â�������ƁA���q�j���m�̔����͂̕��������Ȃ�܂��B
���������āA���鋗���ɂ����Č������ł������Ȃ�A���������肷�邱�ƂɂȂ�܂��B
���ꂪ���q�ԋ��������߂邱�ƂɂȂ�܂��B
�@���̂悤�ȕ��q�O���́A���������q�O���ƌĂ�܂��B
�@�m���ɓd�q�����q�j�ԂɏW��A�o���̌��q�j�������t���邱�Ƃ��\�ƂȂ�܂����A����ł͓d�q���m�̔����͂������Ȃ�̂ł͂Ȃ����ƍl����ł��傤�B �������Ȃ���A�d�q�Ƃ����͔̂g���ł���A���m�Ȍ`�Ƃ������̂�����킯�ł͂���܂���B ����͗ʎq���ɂ���Č��߂���g���ł���A���ꂪ����̏ꍇ�ɂ͈�̓d�q�Ƃ݂Ȃ���邱�ƂɂȂ�܂��B ���������āA��̌��q�O���̏d�ˍ��킹�ɂ���ĐV���ȓd�q�������ƍl����A���̓d�q�ɂ����Ĕ����͂�������Ƃ������Ƃ͂���܂���B ���̔����͂Ƃ����̂́A�قȂ�d�q���m�ɂ���Đ�������̂ł�����A����̕��q�O���ɓ������A�X�s���̈قȂ�d�q���m�ɂ�锽���͂Ƃ������ƂɂȂ�A����͌��q�̑Γd�q�̏ꍇ�Ɠ������ƂɂȂ�܂��B
�@�������A���̂悤�ȓd�q���������ɂł���Ƃ������Ƃł͂Ȃ��A�i����ʒu�ɕߑ�����Ă���Ƃ������Ƃ���j���g���������i���q�O���̈ꎟ�����͂�������܂��j�A�������G�l���M�[��ԂƂ��đ��݉\�Ȃ��̂ƂȂ�܂��B
�@�Ȃ��A���̂悤�Ȃ��Ƃ͌��q�������@�ł͓d�q�̌����Ƃ��Đ�������܂����A���̂��Ƃ͈�̓d�q�������̌��q�O���ɑ��݂���Ƃ������Ƃ��q�ׂ����̂ƍl�����܂��B
�@��L�̌����́A���d�q�̈ʑ����������̂��d�˂��ꍇ�ł����A�ʑ����قȂ�ꍇ�ɂ́A���q�j�Ԃɂ�����d�ז��x���������A�����̌��q�͗�������悤�ɂȂ�܂��B ����́A���̐}�̂悤�ȏ�ԂƂȂ������̂ł��B�@
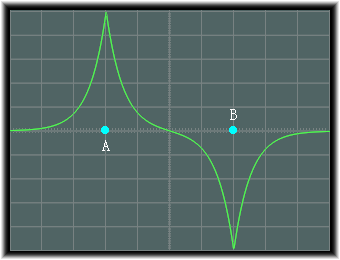
�@���̂悤�ȕ��q�O���́A�����������q�O���ƌĂ�܂��B
�@p�d�q���m�ɂ�鋤�L���� �@s�d�q�ɂ�鋤�L�����ł́A����͋��Ώ̂ł��邱�Ƃ���A�������������܂���B �Ƃ��낪�Ap�d�q���m�̏ꍇ�ɂ͕������������Ƃ���A���̓d�q�̏d�ˍ��킹���ɂ́A2�̏ꍇ������܂��B ��͌������ɑ��ĕ��s�ɂȂ��Č��������킹�ŏd�ˍ��킹����̂ŁA������͌������ɑ��Đ����ɕ���ŏd�ˍ��킹����̂ł��B �O�҂̌����̓Ќ����ƌĂ�A��҂̌����̓Ό����ƌĂ�܂��B �Ȃ��A�Ќ����̏ꍇ�ɂ͌������ɑ��ĉ�]�Ώ̂ƂȂ邱�Ƃ���A�Ђ͑Ώ̐���\��symmetory�𗪂������̂̂悤�ł��B �͕��s����\��parallel�̗��̂悤�ł��B
�@�����̌�����}�Ŏ����ƁA���̂悤�ɂȂ�܂��B

�@�Ќ����̏ꍇ�ɂ́A�������ɑ��ĉ�]�����Ă��\���ȏd�Ȃ肪�ł��邱�Ƃ���A��]�̎��R�x������܂��B
�������A�Ό����̏ꍇ�ɂ͓�̕����ŏd�Ȃ邱�Ƃ���A�����������]������Ƃ������Ƃ͂ł��܂���B
�@�܂��A�Ό����̏ꍇ�ɂ̓Ќ����Ɣ�ׂďd�Ȃ肪�������Ȃ邱�Ƃ���A�����͎キ�Ȃ�܂��B
�@p�d�q��s�d�q����������ꍇ�ɂ́A�Ќ����ƂȂ�܂��B ���̗��R�́A���̃Ό����̏ꍇ�ɂ́A����̈ʑ��͓����ɂȂ��Ă��A�����͈ʑ����قȂ邱�ƂɂȂ邩��ł��B
�@�����O���ɂ�鋤�L����
�@�����O���Ƃ��Ă�s�O����p�O���������������̂���\�I�ŁA����ɂ�sp�����O���Asp2�����O���Asp3�����O��������܂����A���̌`�͂������������ɂȂ�܂��B
�����́A�����z�u�̎d�����قȂ���̂ƂȂ�܂��B
���̍����O���́Ap�d�q�̈���̑��݂̂�c��܂����悤�Ȍ`�ƂȂ邽�߁A�����̓Ќ����݂̂ƂȂ�܂��B
�@�Y�f�̏ꍇ�ɂ́A���̍����O����p�d�q�ɂ���ċ��L�������l���邱�ƂɂȂ�܂��B
���f��_�f�̏ꍇ�ɂ��As�d�q��p�d�q���������邱�Ƃ�����܂����A�T�˂����p�d�q�̃Ќ����̏ꍇ�Ɠ��l�ɂȂ邽�߁A���ɍ����O�����l���Ȃ��Ă���肪�Ȃ����Ƃ������Ƃ����܂��B
�@�����A�Y�f�̏ꍇ�ɂ́A�����O�����l���Ȃ��ƁA�s�Γd�q�̐������̌��q���ł���4�ɂȂ�Ȃ����Ƃ���A�Y�f�ł͍����O���͕K�{�̂��̂ƂȂ�܂��B
�@���d�����@���q����2�ȏ゠����͓̂�d�������s�����Ƃ��ł��A���q����3�ȏ�̂��͎̂O�d�������s�����Ƃ��ł��܂��B
�������A�O�d�����͔�r�I�H�ŁA���d�����̑����͓�d�����ƂȂ�܂��B
�@���d�������s���d�q�͕��ʂɂ�p�d�q�ƂȂ�܂��B
�Ƃ����̂́As�d�q�̏ꍇ�ɂ́A����͕s�Γd�q�͈�����Ȃ�����ł��B
�܂��A����p�d�q������Ȃ�A���̒��O�̋O���ł���s�O���͕��Ă��邱�Ƃ��ƂɂȂ�܂�����A�s��s�d�q�͎����Ă��Ȃ��A�Ƃ������ƂɂȂ邩��ł��B
�@�������A�����O���̂��̂����邱�Ƃ���Ap�d�q�����Ƃ͌���܂���B
�������A�����O���̂��̂̓Ќ������s�����Ƃ͂ł��܂����A�Ό����͍s���܂���B
�@���āA����̌������ɂ��đ��d��������Ƃ����ꍇ�ɂ́A��̓Ќ����ƂȂ�A���̓Ό����ƂȂ�܂��B ���̂��Ƃ́A�Ќ������s���Ă���p�d�q�܂��͍����O���d�q�ɑ��āA����p�d�q�͂����ɑ��Đ����ɂȂ邩��ł��B
�@���̗��R�́A���̂��Ƃɂ��܂��B p�d�q�̔z�u�̎d���́Ax�������Ay�������Az��������3�ɂȂ�܂��B ���q���m��p�d�q���m�ɂ���Č�������Ƃ����ꍇ�A�ŏ��̓Ќ������N����܂��B ���̌��������͂���p�d�q�̕����ƂȂ�܂�����A����p�d�q�͌��������ɑ��Đ����ɂȂ�܂��B ���������āA���̓Ό����ƂȂ�܂��B
�@��L�̂��Ƃ́A�����O���̏ꍇ�ł������ɂȂ�܂��B �Ⴆ�Asp�����O���͈��p�d�q��s�d�q�Ƃ������������̂ł����A���̕����͂���p�d�q�̕����ƂȂ�܂��B ���������āA�����p�d�q�̏ꍇ�Ɠ��l�Ƃ������ƂɂȂ�܂��B �܂��Asp2�����O���́As�d�q��p�d�q2�������������̂ł����A�����2��p�d�q���z�ʂ��镽�ʓ��ɂ���܂��B ���������āA�����O�����`�����Ă��Ȃ�p�d�q�͂���Ɛ����ɂȂ�܂��B �Ȃ��Asp3�����O���́As�d�q��p�d�q3�������������̂ł����A���̏ꍇ�ɂ͕s��p�d�q�͎c���Ă��Ȃ����Ƃ��A���d�����͍s�Ȃ��܂���B
�@���d�����̐����Ƃ��ẮA�Ќ����ɔ�ׂĎア�Ό������ł��邱�Ƃ���A���̕����͑��̕��q�ɂ���ĉ��w�ω����₷���Ȃ�܂��B
���ɁA�_��W�J���̍U�����₷���Ȃ�܂��B
�@�܂��A�P�����̏ꍇ�̃Ќ����ł͌���������]�����邱�Ƃ��ł��܂����A���d�����ł̓Ό������ł��邱�Ƃ���A���̌������͌Œ肷�邱�ƂɂȂ�܂��B
���̂��Ƃ́A�����Y�����f���������b�_�ł͏d�v�Ȃ��ƂƂȂ�܂��B
�Ƃ����̂́A��d���������ꍇ�ɂ͎��R�ɐ܂�Ȃ邱�Ƃ��ł��Ȃ��Ȃ邽�߁A���q�𖧂ɋl�ߍ��ނ��Ƃ��ł��Ȃ��Ȃ邩��ł��B
�܂��A���b�_���m���\���ɐڋ߂ł��Ȃ��Ȃ邽�߁A���q�Ԉ��͂��キ�Ȃ�܂��B
�������A�����������_�́A�t�ɗ��_�ƂȂ�ꍇ������܂��B
2.5 ���L�����̗�
�@�����q�@���̕��q����H2O�ŁA����͎��̂悤�Ɍ������Ă��܂��B
|
�@�A�����j�A�@���̕��q����NH3O�ŁA����͎��̂悤�Ɍ������Ă��܂��B
|
|
�@�i�q�G�l���M�[
�@�C�I�������̏ꍇ���������������ꍇ�ɂ͌����G�l���M�[�������܂��B
���̂��߁A�����̃C�I�����q�ɂ���ăC�I���������`�������ƁA�M�����邱�ƂɂȂ�܂��B
�@�C�I�������̏ꍇ�A�z�C�I���ƉA�C�I�������݂ɕ��ь����i�q���`�����܂��B
0K�ɂ����āA���ꂼ��̃C�I��1mol�����������̂ɕK�v�ȃG�l���M�[�̂��Ƃ͊i�q�G�l���M�[�ƌĂ�܂��B
�@�C�I�����f
�@�A�C�I�����`�����錳�f�́A1�̓d�q������A����Ȋk�\�����`������n���Q�����f����\�I�ŁA����̓t�b�fF�A���fCl�A�L�fBr�A���E�fI�A�A�X�^�`��At�ƂȂ�܂��B
�܂��A2�̓d�q���������Ȋk�\�����`�����āA2���̉A�C�I���ƂȂ�_�f��C�I�E������܂��B
�@�z�C�I�����`�����錳�f�́A1�̓d�q�������Ĉ���Ȋk�\�����`�����鐅�f�ƃA���J���������f�i���`�E��Li�A�i�g���E��Na�A�J���E��K�A���r�W�E��Rb�A�Z�V�E��Cs�A�t�����V�E��Fr�j����\�I�ł��B
�܂��A2�̓d�q�������Ĉ���Ȋk�\�����`������A���J���y�ދ������f�i�x�����E��Be�A�}�O�l�V�E��Mg�A�J���V�E��Ca�A�X�g�����`�E��Sr�A�o���E��Ba�A���W�E��Rd�j������܂��B
���ɂ́A�A���J���������f�Ǝ������f�̓�Cu��A�A���J���y�ދ������f�Ǝ������f�̈���Zn�A�J�h�~�E��Cd�A����Hg������܂��B
3.1 �C�I�����a
�@�z�C�I���ƉA�C�I���Ƃł́A�ǂ��炪�傫�����Ƃ������ƂɂȂ�܂����A����͕��ʂɂ͉A�C�I���ɂȂ�܂��B
�Ⴆ�A�ł��������A�C�I���ł���t�b�f�̃C�I�����a��1.36���i�I���O�X�g���[���j�ł����A�i�g���E���C�I���̃C�I�����a��0.95���ƁA�t�b�f��70%�قǂɏk�����Ă��܂��܂��B
�������A�z�C�I���̃Z�V�E���C�I���̏ꍇ�ɂ́A�C�I�����a��1.69���ƂȂ�A����̓t�b�f�C�I�������傫���Ȃ�܂��B
�@�C�I�����a�́A�C�I���������`�����Ă���z�C�I���ƉA�C�I���̊j�ԋ����������̃C�I�����a�̘a�ƂȂ�悤�ɒ�`����Ă��܂��B
�@�C�I�������̍\���@����͗z�C�I���ƉA�C�I���̃C�I�����a�̔�ɂ���āA��̐��肷�邱�Ƃ��ł��܂��B
�����ŁA�ȉ��ł͂��̂��Ƃɂ��Đ������܂��B
�@���̎��A��~�ɐڂ��鏬�~�̔��a���A���̍\���ł̍ŏ��̃C�I�����a��Ƃ������ƂɂȂ�܂��B
���̔��a��ς����߂邽�߂ɁAA�̉~�ɂ��Ă̎��̐}���l���܂��B
�@������A���̂悤�� �ς����߂��܂��B
�@�ȉ��ɁA�A�C�I���̕����傫���Ȃ闝�R���L�q���Ă����܂��B
�@���āA�A�C�I���Ƃ����̂́A�d�q����܂��͓������āA����ȓd�q�k���`�����ꂽ���̂ł��B
����A�z�C�I���͂��̋t�ŁA�d�q����܂��͓�������āA����ȓd�q�k���`�����ꂽ���̂ł��B
�i�������A��O�I�ɋ��L�������������Ă���ꍇ������܂��B�j
�@�A�C�I���ł͓d�q�������邱�Ƃɂ���āA�d�q�ɂ��Օ������܂�A�L���j�d�ׂ��������Ȃ�܂��B
���̂��߁A�ŊO�k�̓d�q�̔��a�͑傫���Ȃ�܂��B
�i���q���a�ɂ��ẮA���q�O����5.5b�����Q�Ƃ��ĉ������B�j
�@�z�C�I���̏ꍇ�ɂ́A�d�q�����邱�Ƃɂ���āA�L���j�d�ׂ��������Ȃ�܂�����A���̔��a�͑傫���Ȃ�܂��B
�@�k���`�����Ă���d�q�k�́A���̔��a�̑傫���ɉ����ĕς锤�ł�����A�A�C�I���ł͑傫���Ȃ�A�z�C�I���ł͏������Ȃ�A�ƍl�����܂��B
�܂��A�k�ƂȂ����d�q�k�́A�k�̓����܂œ��荞�ނ悤�ɐڋ߂���Ƌ����˗͂������܂��B
�i���̂��Ƃ̓t�@���f�����[���X�����͂ɂ��܂��B�j
���������āA�C�I�����a�͊O���̓d�q�k�̔��a�i����̓t�@���f�����[���X���a�ɂȂ�܂��j�����������Ȃ邱�Ƃ͂���܂���B
�@�܂��A�C�I�������̓N�[�����͂Ō����������̂ł�����A�A�E�z�̃C�I���͂ł��邾���ڋ߂��悤�Ƃ��邱�ƂɂȂ�܂����A���̐ڋߋ����̓t�@���f�����[���X�����͂ɂ��t�@���f�����[���X���a�����킸���ɑ傫���Ȃ�܂��B
�@���������āA�C�I�����a�͌��q���a�̑傫���ɑ��ւ���Ƃ������ƂɂȂ�܂��B
�@�C�I���̌����\�������߂�̂͑傫�����̃C�I���̔z�u�\���ƂȂ邽�߁A�������ɂ��čl���邱�Ƃɂ��܂��B
���ɂ���͔̂��a��i���������̃C�I�����a�^�傫�����̃C�I�����a�j�ł�����A����a�P�̋��Ƃ��܂��B
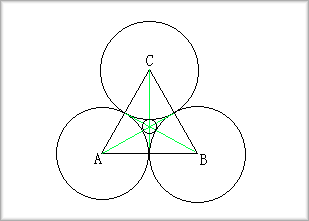
�@����̑傫���̋����[�U������ꍇ�A���ꂪ�ł��f���ɂȂ�z�u�́A���O�p�`�z�u�ł���A����͎��̂悤�ɔz�u���邱�ƂɂȂ�܂��B
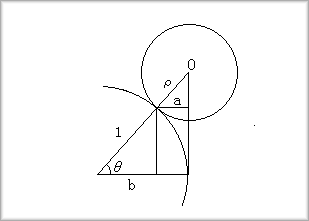
| (3.1) |
�@�p�Ƃ́A���O�p�`�̏ꍇ�ɂ�30�K�ƂȂ邱�Ƃ���A�ς�0.1547�c�ɂȂ�܂��B
�@�����f���Ȕz�u�͐��l�ʑ̂ƂȂ邱�Ƃ��A���̐}���l���܂��B
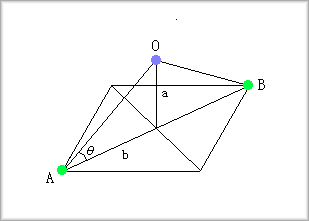
�@�����ŁAA�CB�͎l�ʑ̔z�u������ꍇ�̂S�̋��̓��̂Q�̋��̒��S�ł��B
�܂��AO�͎l�ʑ̂̒��S�ƂȂ�܂��B
�����̂̈�ӂ̒������P�Ƃ���ƁAa�̒�����1/2�Cb�̒����́�2/2�ƂȂ邱�Ƃ���A�Ƃ�tan-1(1/��2)��36.264�c�K�ƂȂ�܂��B
�@���̏ꍇ�����O�p�`�̏ꍇ�Ɠ����悤�ɁA�O�p�`OAB���l����ƁA���̔��a��ς�0.2247�c�ƂȂ�܂��B
�@�����f���Ȕz�u�͐����ʑ̂ł���A���̏ꍇ�ɂ͏��������̃C�I�������̂悤�ɔz�u���邱�ƂɂȂ�܂��B
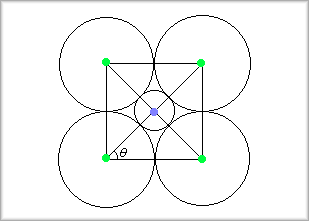
�@���̏ꍇ�ɂ́A��=45�K�ƂȂ�܂�����A�ς�0.4142�c�ƂȂ�܂��B
�@�����ʑ̂̎����f���ƂȂ�z�u�́A���Z�ʑ́i�����́j�ƂȂ�܂��B ����ɐڂ��鏬�~�̔��a�����߂邽�߂ɁA���̐}���l���܂��B
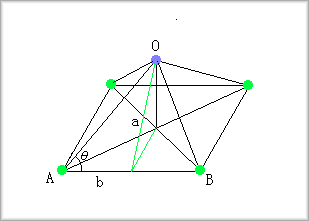
�@�����ŁA�O�p�`OAB���l����ƁAa�̒����́�2/2�Cb�̒�����1/2�ł�����A�Ƃ�tan-1(��2)=54.73561�c�K�ƂȂ�܂��B ���������āA�ς͖�0.732�ƂȂ�܂��B
�@�ȏ�̂��Ƃ��܂Ƃ߂�ƁA�C�I�������̍\���̓C�I�����a�̔���A���̂悤�ɂȂ�܂��B
| ���a�̔䗦 | ���̔z�u | �z�ʐ� | ���l |
|---|---|---|---|
| 1 | �������ʑ� | 12 | ���̔z�u������ |
| 1�`0.732 | ������ | 8 | �@ |
| 0.732�`0.414 | �����ʑ� | 6 | NaCl�Ȃ� |
| 0.414 | �����` | 4 | ���̔z�u������ |
| 0.414�`0.225 | ���l�ʑ� | 4 | �@ |
| 0.225�`0.155 | ���O�p�` | 3 | �@ |
4. ��������
�@���L������C�I�������̏ꍇ�ɂ́A�d�q�͈�̌��q�܂��͏����̌��q�ɕߑ����ꂽ���̂ł����B
�����ɑ��ċ��������́A�d�q�������̌��q�ɑ�������Ȃ��ŁA���̋������̌��q�Ԃ����R�ɉ^������d�q�ɂ���Č����������̂ł��B
�@�������`�����錳�f�Ƃ��ẮA�A���J�������A�A���J���y�ދ����A�J�ڋ�������\�I�ł��B
�����́A���̂悤�ȓ���������܂��B
�@��L�ȊO�ɂ́A12���̈����E�J�h�~�E���E�����A3p�d�q�����A���~�j�E���A4p�d�q�����K���E���E�Q���}�j�E���A5p�d�q�����C���W�E���E�X�Y�E�A���`�����A6p�d�q�����^���E���E���E�r�X�}�X�E�|���j�E��������܂��B
�@�����̍\�����ȒP�ɏq�ׂ�Ȃ�A����͓��팳�f���m�̌����ɂ���ē���̌��q����d�q������������Ă�����̂Ƃ������ƂɂȂ�܂��B
����͎��̏��l����Ζ��炩�Ȃ��ƂɂȂ�܂��B
���̂悤�ɓ���̌��q�j�������I�ɕ��z���Ă���ꍇ�ɂ́A�d�q�͊e���q�j�̒��ԂɈʒu����̂����R�Ȕz�u�ɂȂ�܂��B
���̂��Ƃ͊e���q���z�C�I�������ēd�q����o���Ă���ƍl���邱�Ƃ��ł��܂����A������͓���̌��q�j����Ȃ�i�q�̒��ɓd�q�����V���Ă���ƍl���������A���R�Ȍ����ɂȂ�܂��B
�@���āA���������̎�舵���ɂ��ẮA���q�O���@�ƌ��q�������@�ł̋��ɂ���čl��������\�I�ł��B
�܂��A���̏ꍇ�����q�I�����Ɣg���I����������܂��B
�@���R�d�q�̔g����
�@�����������R�ɓ�����鎩�R�d�q�Ƃ͉����Ƃ������ƂɂȂ�܂����A����͔g���I�ɂ͔�Ǎݓd�q�̂��ƂɂȂ�܂��B
�d�q�̔�Ǎݐ��͓q���q�̌��������q�O���ł������܂������A���̂��Ƃ͌��q�O���̏d�Ȃ�ɂ����̂ł��B
�܂�A�o���̌��q�O�����d�Ȃ邱�Ƃɂ���Č��q�Ԃɂ����z���邱�Ƃ��ł��A�d�q�͓�̌��q�j�̎�����^�����邱�ƂɂȂ�܂��B
���̂悤�ȏd�Ȃ肪�e���q�ɂ����Đ�����ƁA��̑傫�ȕ��q�O�����`�����邱�ƂɂȂ�܂��B
4.1 �����̌����\��
�@�����͂ł��邾���f���Ȕz�u���Ƃ�悤�ɂȂ�܂����A����Ƃ��Ă͑̐S�����A�ʐS�����A�Z���f���̎O�킪����܂��B
���̒��ł́A�ʐS�����ƘZ���f���ł́A���q�̐�߂銄����74%�ƍł��f���ɂȂ�܂����A�̐S�����̏ꍇ�ɂ�68%�ɂȂ�A��⌄�Ԃ��ł��܂��B
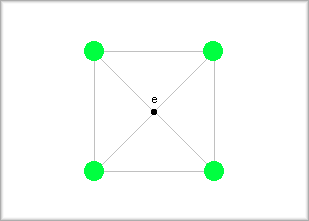
�@�ʐS�����̏ꍇ�ɂ́A���̂悤�ɂȂ�܂��B
���̏ꍇ�������̂̈�ӂ̒�����1�Ƃ��܂��B
���̂���ʂ̑Ίp���̒����́�2�ɂȂ�܂�����A����ɓ��鋅�̔��ar�́A��2/4�ɂȂ�܂��B
�܂��A���̗����̂ɓ��鋅�̐���4�ɂȂ�܂�����A���̑S�̐�V�͎��̂悤�ɂȂ�܂��B
�Ȃ��A�Z���f���^�ŁA�^�̋t�O�p�`�̔z�u�͎O�p�`�̔z�u�ɂ��Ă��������ƂɂȂ�܂��B
���������āA�Z�p�`�{�t�O�p�`�i�O�p�`�j�{�O�p�`�i�t�O�p�`�j�{�Z�p�`�Ƃ����z�u���A���l���f���ɂȂ�܂��B
���́A����͖ʐS�����^��45�K�̊p�x�Ő������i�Ⴆ�A�E�㉜�̗̋�����Q�̐��F�̋���ʂ��Đ���܂��j�z�u�ɂȂ�܂��B
�i���ۂɋ�����ׂĂ݂Ȃ��ƍl���ɂ����ł����B�j
�@�̐S�����^�ɂ̓��`�E���A�i�g���E���A�J���E���Ȃǂ�����܂��B
�ʐS�����^�ɂ́A�A���~�j�E���A�J���V�E���A���A���Ȃǂ�����܂��B
�Z���f���^�ɂ́A�x�����E���A�}�O�l�V�E���A�����A�J�h�~�E���Ȃǂ�����܂��B
�@�����̎d���̓C�I�������Ǝ��Ă��܂����A�A�C�I���ɑ������鎩�R�d�q�͔��ɍ����ɉ^�����Ă��邱�Ƃ���A�e���q�̔z�u�]�ڂɑ��đ��₩�ɉ������邱�Ƃ��ł���_���A�C�I�������Ƃ̑傫�ȈႢ�ƂȂ�܂��B
���̂��߁A�����͑傫�ȋ��x�����Ɠ����ɂ��Ȃ₩���������ƂɂȂ�܂��B
�@�܂��A���R�d�q�͓d��̉e�����ĉ^�����s���܂�����A�d���d����`������̂ƂȂ�܂��B
�܂��A����͔M�G�l���M�[��`������A�z�������肵�āA�M�̓`�����s�����̂ƂȂ�܂��B
�����̕��� ���� �A���J������ �ŊO�k�ɕs��s�d�q�݂̂����B �A���J���y�ދ��� �ŊO�k��s�d�q�݂̂����B �J�ڋ��� �ŊO�k��nd�d�q�������A(n+1)p�d�q�������Ȃ��B
�܂��A�����̂��̂�(n+1)s�d�q�����B
�@�ȏ�̌��f�͔�r�I�e�ՂɃC�I�����ł���Ƃ������Ƃ��A���ʓI�ȓ����ƂȂ��Ă��܂��B
�@�������A�d�q�͉^�����Ă��܂�����A���鎞�ɂ͂��錴�q�̑��ɂ���A���q�Ɓu�������Ă���v�ƍl���邱�Ƃ��ł��܂��B
����������͈ꎞ�I�Ȃ��̂ł���A���̌����͉��z�I�Ȃ��̂Ƃ������Ƃ��ł��܂��B
�@���̂悤�ȗz�C�I���͋^���I�Ȃ��̂ŁA�{���̗z�C�I���ł͂���܂���B
�Ƃ����̂́A����͒P�ɓd�q�̉^���ɂ���Ĕz�u�̕肪���������̂ɂ����Ȃ�����ł��B
����ŁA�z�C�I�����ł���Ȃ�A�����ɂ͉A�C�I�����ł��A�����͑��E����܂��B
�@�܂��A���R�d�q���{���̃G�l���M�[�������Ă���킯�ł͂Ȃ��A�������Ƃ����G�l���M�[�̒Ⴂ�̈���ł̉^���Ƃ������Ƃɂ����܂���B
�����Ⴆ��Ȃ�v�[���̒�ł̓d�q�̎��R�^���Ƃ������Ƃł���A�d�q���G�l���M�[�Č��q�̑������痣��Ď��R�^�������Ă�����̂ł͂���܂���B
�@�����̍\���́A�ȉ��̔z�u�ɂȂ�܂��B
�@�̐S�����̏ꍇ�ɂ́A���̂悤�ɂȂ�܂��B
�܂���ӂ̒�����1�̗����̂��l���܂��B
���̗����̂̑Ίp���̒����́�3�ɂȂ�܂�����A����ɓ��鋅�i�[�̏ꍇ�͋��̒��S�Ƃ��܂��j�̔��ar�́A��3/4�ɂȂ�܂��B
�܂��A���̗����̂ɓ��鋅�̐��́A���̂悤�ɂȂ�܂��B
���������āA���̗����̂ɓ��鋅�̑S�̐�V�͎��̂悤�ɂȂ�܂��B
4
����
8�{1�{
4
����
8��2
V��2�
4pr3
������
3��2�
4p�(��3)3
����������������
3�43��0.6802
V��4�
4pr3
������
3��4�
4p�(��2)3
��������������
3�43��0.7405
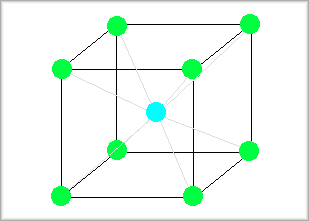
�̐S�����^ 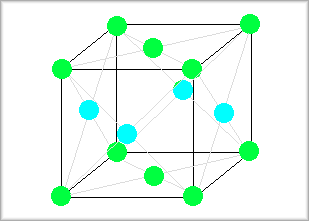
�ʐS�����^ 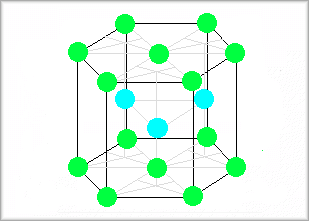
�Z���f���^
|
�Ձ�c1��1�{c2��2�{c3��3�{�c | (4.1) |
�@n�̌��q�O���ɑ��Ă�n�̕��q�O�����Ή����邱�ƂɂȂ�܂����A����ɂ͌������̂��̂Ɣ��������̂��̂�����܂��B
�������̕��q�O���Ƃ����̂́A���q�O�������G�l���M�[���ʂ��Ⴍ�Ȃ���̂ŁA���������̕��q�O���́A���q�O���̃G�l���M�[���ʂ��������Ȃ���̂������܂��B
�������A���q�O���̏d�Ȃ肪�Ȃ��ꍇ�ɂ́A����͌X�̌��q�O���Ƃ������ƂɂȂ�܂�����A����͌��q�O���̃G�l���M�[���ʂƓ����ɂȂ�܂��B
�@�Ⴆ�A�Q���q�̏ꍇ�ɂ́A���q�O���Ղ͎��̂悤�ɂȂ�܂��B
|
��-��s(1)�|s(2) ��+��s(1)�{s(2) |
|

�@���ɁA4���q�is(1)�Cs(2)�Cs(3)�Cs(4)�̏��ŕ���ł���Ƃ��܂��j�̏ꍇ�ɂ́A���̕��q�O�����Ƃ邱�ƂɂȂ�܂��B
|

���̂悤�ɁA��1�ł́A�S�Ă��������I�d�Ȃ�ƂȂ�܂��B
��2�ł́A��̔������I�d�Ȃ�ƈ�̌����I�d�Ȃ肪�ł��܂��B
��3�ł́A��̌����I�d�Ȃ�ƈ�̔������I�d�Ȃ肪�ł��܂��B
��4�ł́A�S�Ă������I�ƂȂ�܂��B
�Ȃ��A��2�ł�-��2�̏ꍇ���l�����܂����A����͒P��-1���|�������̂Ȃ̂ŁA����͏��O����܂��B
��3�����l�ł��B
�@���l�ɑ����̌��q�ɂ��čs�����ꍇ�̃G�l���M�[���ʂ͎��̂悤�ɂȂ�܂��B
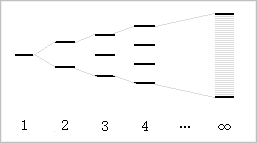
�@���̐}�̂悤�ɁA���悻�����Ƃ����邭�炢�����̌��q�̌��q�O�����d�˂��e���q�O���̃G�l���M�[���ʂ͘A���I�ɕ��Ԃ��ƂɂȂ�܂��B ���̘A���I�ȃG�l���M�[���ʂ̗̈�̂��Ƃ̓G�l���M�[�o���h�܂��͒P�Ƀo���h�ƌĂ�܂��B
4.2.2 ���������̋���
�@���������q�O���@�ɂ���čl�����ꍇ�̋��������̋����ɂ��ďq�ׂĂ����܂��B
��ʓI�ɕ��q�O���̓��A�����͌������O���ƂȂ�A�����͔��������O���ƂȂ�܂��B
�e���q�O���ɂ͔r�������ɂ���܂ł̓d�q�������邱�Ƃ��ł��܂���B
���������āA���������������s���A����d�q���S�đΓd�q�݂̂̏ꍇ�ɂ́A�������O���Ɣ��������O�����S�Ė��܂邱�ƂɂȂ�A���̓d�q�ɂ���Ă͌��q���m�͌������Ȃ����ƂɂȂ�܂��B
4.3 �A���J���y�ދ���
�@�A���J���y�ދ�����2���̌��f�ŁA����͍ŊO�k�ɑ�2s�d�q�݂̂������f�ł��B
�̓d�q�ł͋��L�������s�����Ƃ͂ł��Ȃ����߁A���2p�O���ɏ��ʂ��邱�ƂɂȂ�܂��B
�i��s�d�q�ɂ���Ă͕��q�O���@�ł������������s�����Ƃ͂ł��܂���B�j
���̌��ʁA2s�d�q��2p�d�q���ł��邱�Ƃ���Asp�����O�����`�����邱�ƂɂȂ�܂��B
�����2�������̂��̂ł�����A
�Ƃ����������`�����邱�ƂɂȂ�܂��B
�@���sp�����O���ɂ��A��������̌����ɑ��錋���\���͘Z���f���^�ɂȂ�ƍl�����܂����A�x�����E���͐��ɂ��̔z�u�ɂȂ��Ă��܂��B
�܂��A�����̃}�O�l�V�E���̏ꍇ���Z���f���^�ƂȂ�܂��B
�@�������A�J���V�E���ȍ~�ɂȂ�ƃx�����E����}�O�l�V�E���̏ꍇ�Ƃ͏��قȂ�܂��B
�Ƃ����̂́A4�����ȍ~�ł́A�܂��ŏ���3d����̏��ʂ�4s�O������l�܂邩��ł��B
���������āA���̉��ʂɂ�3d�O��������܂��B
���̂��߁A��4s�d�q�̈��3d�O���Ɂu���ʁv���邱�ƂɂȂ�Asd�����O���ɂ���ċ��L�������s�Ȃ���ƍl�����܂��B
4.3.1 �����O��
�@�x�����E���̏ꍇ�ł͋������������q�������@�ōl�����킯�ł����A����ɂ���ċ����̎��R�d�q���ǂ��l���邩�Ƃ������Ƃɂ��ďq�ׂĂ����܂��B
4.4 �J�ڌ��f
�@�J�ڌ��f�͍ŊO�k��d�O����f�O���������Ap�d�q�������Ȃ����f�ł��B
�������A�ŊO�k��d�O����s�O�����O�a���Ă��Ȃ����f�ł��B
4.4.1 �J�ڌ��f�̐���
�@�J�ڌ��f�̋����̐����Ƃ��ẮA�ȉ��̂��̂�����܂��B
�@1) �Z�_�������B�d�x���傫���B
�@�����ŁA�Ⴆ��4�����̋������f����уA���S���i�t�@���f�����[���X�̗͂�j�̗Z�_�ƕ��_�ׂ�ƁA����͎��̂悤�ɂȂ�܂��B
���̕\�ŁA�d�q����( )���̐����͕s�Γd�q���ł��B
�@�Ƃ���ŁA�J�ڌ��f�Ƃ��Ă͓��������̂��錳�f�ł����A����̌����̎d�����ǂ��Ȃ邩�Ƃ������Ƃ��q�ׂĂ����܂��B
���̏ꍇ�ɂ́A3d104s1�ł�����A�P���ɂ͂����d�d�q�k���`������āA����������4s�d�q�ɂ���čs�Ȃ���ƍl���邱�Ƃ��ł��܂��B
�������A����ł����q�ԋ����╦�_�̍�����������邱�Ƃ�����Ȃ�܂��B
�@�����5�̓d�q�ɂ���č����O�����`������A���̌��q�ƌ������s�����ƂɂȂ�ƍl����A���q�ԋ����̒Z��������ł��܂��B
�܂��A�Z�_�╦�_����r�I�����̂��������邱�Ƃ��ł��܂��B
�@�A���J�������̏ꍇ�ɂ�s�d�q�݂̂����������ƊW���邱�ƂɂȂ�܂����A���̏ꍇ�ɂ͌��q�ԍ����傫���Ȃ�قǗZ�_��������܂��B
���̂��Ƃ͓��k�̓d�q�����傫���Ȃ�A���q�j�̗L���j�d�ׂ��������Ȃ邱�Ƃ��W���Ă���ƍl�����܂��B
���̂��Ƃ́A�ȉ��ɂ��܂��B
�@�����ŁA�����ɂ�����d�d�q�̏ꍇ��1���̃A���J�������̏ꍇ�Ɠ����悤�ɂȂ邩�Ƃ����A�K���������̂悤�ɂ͂Ȃ�܂���B
4���ȍ~�ɂȂ�ƁA��̎����قǗZ�_�������Ȃ�܂��B
�@���̂��Ƃ́Ad�d�q���������Ă����q�j�̗z�d�ׂ̎Օ����̑�����́A�z�q���̑���̕��������Ă��邽�߂ƍl�����܂��B
�Ȃ��Ȃ�A�d�q���m�̔����ɂ��A���̓d�q�͉��������ɒǂ�����A���̓d�ׂ̒��S�ʒu�͌��q�j���������Ȃ邩��ł��B
�܂�A1�̓d�q�̕��d�ׂ̐˗͂���1�̗z�q�̈��͂̕��������Ȃ�܂��B
���̂��Ƃ́A��2�������3�����Ō��q�ԍ���������قǁA�܂�p�d�q��������قǓd�C�A���x�������Ȃ�̂Ɠ������Ƃł��B
�@�j�d�ׂ̑���Ɠd�q�ɂ��Օ��̊W�ɂ��ẮA���̐}������Ε�����Ղ����Ǝv���܂��B
�@s�d�q��p�d�q�̏ꍇ�ɂ́A�����ɓd�q�k���ł���ƁA�C�I�����G�l���M�[���������邱�ƂɂȂ�܂��B
�܂�A�j����̈��͂��������邱�ƂɂȂ�܂��B
���̗��R�́A�����̓d�q�ɂ���Ċj�d�ׂ́u�Օ��v�������邽�߂ł��B
�@2) �L�@�������ƌ������āA���̂����B
�@3) �_�ɗn����B
�@4) �펥���������B
�@���āA���C�o�Ɏq�͓d�q�̉�]�^���ɂ���Đ�����ꍇ�ƁA�X�s���ɂ���Đ�����ꍇ�̓������܂��B
�C�̌��q�̏ꍇ�ɂ́A���q�̉�]�����R�ł��邱�Ƃ���A�O���p�^���ʂɂ�鎥�C�o�Ɏq������̕������������Ƃ��ł��܂����A�����̏ꍇ�ɂ́A���q���m�͌������Ă��邱�Ƃ���A���R�ɉ�]���邱�Ƃ͂ł��Ȃ��ƂȂ�܂��B
���������āA���̏펥���̓X�s���ɂ���Đ����邱�ƂɂȂ�܂��B
�@�����ŁA�����������S�̏ꍇ�ɂ��ďq�ׂ邱�Ƃɂ��܂��B
���̌��q�̍ŊO�k�̓d�q�͎��̔z�u�ɂȂ�܂��B
���̊e�Γd�q�������ɂ���āA���̂悤�ɗ�N���邱�ƂɂȂ�܂��B
���̂悤�ɕs�Γd�q��8�ł��܂����A�S�̎��ۂ̌��q���́A���q�ԋ�������5.8�ł���Ƃ���i���m�ɂ�������͋��L�d�q�ɂ�錴�q���̂��ƂŁA����ȊO�̈�d�q�����Ƃ����̂��܂߂�Ɩ�6�ɂȂ�܂��j�A���������āA���ς���2.2���s�Γd�q�Ƃ��Ďc�邱�ƂɂȂ�A���ꂪ�������������ƂɂȂ�܂��B
�@�Ȃ��A�i4�`5�����́j�J�ڋ����̋��������̏ꍇ�A�ŊO�k�ɓd�q�����e�����O�����́Ad�O��5�{s�O��1�{p�O��3��9�ł͂Ȃ��A�Q�l����8�ɂ��Ƒ��8.3�ɂȂ�Ƃ���܂��B
���������āA���ꂩ�猴�q���d�q��6���������A2.3�����q���s�Γd�q�Ƃ��Ďc��d�q���̍ő�l�ƂȂ�܂��B
�@���̂悤�Ȍ��f�̑�\�Ƃ�������̂�����ł��B
����́A�ŊO�k��5d106s2�̓d�q�z�u�������̂ł��B
����͗Z�_����-39���ŁA�퉷�ŗB��t�̂ƂȂ��Ă�������ł��B
�i�Ȃ��A���h���̗Z�_�͖�-71���ł��邱�Ƃ���A���̌����͎͂�Ƀt�@���f�����[���X�͂ł���ƍl�����܂��B�j
�܂��A�����̈�����J�h�~�E�����Z�_���Ⴍ�A����̏ꍇ�Ǝ��Ă��܂��B
�@���̂悤�Ȕz�u���������邱�Ƃ���A�����̌����̎d��������A�����͋������̂���邱�ƂɂȂ�܂��B
���̂��Ƃ͋������������q�������@�ɂ���Đ���������̂ł����A���ꂾ���ł͓d�C�`���̐����͍���Ȃ��߁A�C�I���̂��̂�����ƍl���܂��B
���̕��C�I���̏ꍇ�ɂ́Asp2�����O�����`�����邽�߁A����ɂ�錋���͕��ʓI�ȎO�������̌����ƂȂ�܂��B
������l�X�Ȕz�u�̂��̂��l�����邱�Ƃ���A�����G�ɂȂ�܂��B
�@�܂��A���w�I�������A�J���V�E���ȍ~�̓T�^�I�ȃA���J���y�ތ��f�ƃ��`�E���E�}�O�l�V�E���Ƃł͈قȂ�܂��B
���̂��߁A�����͓������ł��ʂ̎�ނɂȂ�܂��B
�@�ȒP�ȋ����̗�Ƃ��ă��`�E�����l���A���̋��������ɂ��Đ������܂��B
���q�������@�ł́A���������͋��L�����̋������̂Ƃ��čl���܂��B
���̂悤�Ȃ��͉̂��z�I�Ȃ��̂ł���A�����ƑΉ��������̂ł͂���܂��A�d�q�ɂ�鋤�L�����ɂ���čl���邱�Ƃ��ł��邽�ߗL�p�Ȃ��̂Ƃ������Ƃ��ł��܂��B
�@�܂��A�C�I���������Ă��Ȃ��ꍇ�ɂ́A���̂悤�ȋ������̂������Ă��܂��B
Li �� Li Li �@ Li �C �� �@ �� Li �� Li Li �@ Li
Li �� Li- �� Li+ Li
�@���̂悤�ɁA���錴�q�����̌��q�̓d�q�i���R�d�q�j�������悤�ȋO���̂��Ƃ͋����O���ƌĂ�A���q�O���̃G�l���M�[���ʂɋ߂��O���ɂȂ�܂��B
���`�E���̏ꍇ�ɂ́A�����2���̌����̂��̂Ƃ������ƂɂȂ�܂�����A2p�O���ƂȂ�܂��B
����ɁA�����s�O����p�O���̍����������āAsp�����O���ƂȂ�܂��B
�@���������̏ꍇ�ɂ́A���̂悤�ȋ����O�����K�v�ɂȂ�܂��B
���������āA��r�I�߂��G�l���M�[���ʂ̋O���S�Ă͎g�p�ł��Ȃ��ƂȂ�܂��B
�܂��A1���q����u���v�̋����O�������邩�ɂ���āA���R�d�q�̐�������܂��B
�@���������̏ꍇ�A��ʓI�ɂ͍ŊO�k�̓d�q�́A�i���q�������@�ł́j���L�����d�q�i���q���d�q�j�A�L�����d�q�i�Γd�q�̏ꍇ�ƕs�Γd�q�̏ꍇ������܂��j�A���R�d�q�ɋ�ʂ���܂��B
�@d�d�q�i��f�d�q�j�������Ƃ̈Ӗ��́A����炪s�d�q�Ɠ����悤�Ɏ���̌��q�Əd�Ȃ肪�����邱�ƂƁA�O���̐��������Ƃ������Ƃł��B
�O���̐��������Ƃ������Ƃ͕s�Γd�q�����ꂾ���������Ă�Ƃ������Ƃ��Ӗ����A���������Č������̋����������s���d�q�������Ƃ������ƂɂȂ�܂��B
���̂��Ƃ��A�J�ڌ��f�ɂ���������̐��������������̂ƂȂ�܂��B
�@�����̂��Ƃ́A�s�Γd�q�������ꍇ�ƂȂ�܂��B
���q�O���@�ōl�����ꍇ�A�s�Γd�q������Ƃ����ꍇ�ɂ́A���q�O������������Ȃ��Ƃ������Ƃł�����A���������O���ɓ��鐔�����������O���ɓ��鐔�̕����������ƂɂȂ邩��ł��B
�܂��A���q�������@�ōl�����ꍇ�ɂ́A���L�����ł���d�q�̐��������邱�Ƃɂ��܂��B
�@���ɁAd�O���̏ꍇ�ɂ͋O�������������Ƃ���A�s�Γd�q���������Ȃ�܂��B
�܂��A��ʂ̋O���Ƃ̃G�l���M�[�����������Ȃ邱�Ƃ���A���̋O���ւ̏��ʂ��e�Ղł���Ƃ������Ƃ��W���Ă��܂��B
���������āA����Ԃł͕s�Γd�q�������Ȃ��ꍇ�ł��A�����G�l���M�[���ʂ̋O���ւ̏��ʂɂ���ĕs�Γd�q���������܂��B
���̂��Ƃ́Ad�O�������J�ڋ����ł́A�G�l���M�[���ʂ���r�I�߂���ʂ�s�O����p�O���ɓ��邱�Ƃ��ł��邽�߂ł��B
�@�������Ad�O�����s�Γd�q�ɂ���Ė������ꂽ�}���K���ł́A�s�Γd�q�������ɂ��ւ�炸��O�I�ɉ�����܂��B
���f �d�q�� ���q�Ԋu
�~10-10m�Z�_
K�i���j���_
K�i���j�����\�� ���l 3d 4s 4p 18 Ar(�A���S��) �@ �@ 84(-189) 87(-186) �ʐS���� ��K�X���f 19 K(�J���E��) 0 1 0 4.544 337(64) 1047(774) �̐S���� �A���J���������f 20 Ca(�J���V�E��) 0 2 0 3.947 1112(838) 1757(1480) �ʐS���� �A���J���y�ދ������f 21 Sc(�X�J���W�E��) 1 2 0 3.256 1814(1541) 3104(2831) �ʐS���� �J�ڌ��f 22 Ti(�`�^��) 2 2 0 2.896 1998(1725) 3560(3287) �Z���f�� 23 V(�o�i�W�E��) 3 2 0 2.622 2160(1887) 3650(3377) �̐S���� 24 Cr(�N����) 5 1 0 2.498 2130(1857) 2945(2672) �̐S���� 25 Mn(�}���K��) 5 2 0 2.731 1517(1244) 2235(1962) �l�X 26 Fe(�S) 6(4) 2 0 2.482 1808(1535) 3023(2750) �̐S���� 27 Co(�R�o���g) 7(3) 2 0 2.506 1768(1495) 3134(2861) �Z���f�� 28 Ni(�j�b�P��) 8(2) 2 0 2.492 1726(1453) 3005(2732) �ʐS���� 29 Cu(��) 10(0) 1 0 2.556 1357(1083) 2840(2567) �ʐS���� 30 Zn(����) 10 2 0 2.665 693(420) 1180(907) �Z���f�� �@ 31 Ga(�K���E��) 10 2 1 2.442 303(30) 2676(2403) �@ �@ 32 Ge(�Q���}�j�E��) 10 2 2 2.450 1211(937) 3103(2830) �l�p�� ���q���������f 33 As(�q�f) 10 2 3 2.495 1090(817) 889(616) �@ 34 Se(�Z����) 10 2 4(2) 2.321 490(217) 958(685) �@
�@���̕\�̂悤�ɁA�����̌����͂͌��q�Ԋu�i���q�ԋ����j�ƕs�Γd�q���ƊW���Ă��邱�Ƃ�������܂��B
���̎����̑J�ڌ��f�ł́A�o�i�W�E���ɂ����ėZ�_����ѕ��_���ɑ�������܂����A���̂��Ƃ�4s�d�q��3d���ʂւ̏��ʁi���f�ɂ����4s�d�q��3d�d�q�̃G�l���M�[���ʂ͕ς�܂��j���W���Ă���ƍl�����܂��B
�܂�A���̏ꍇ�̕s�Γd�q���́A4s�d�q1��3d�d�q4�A�܂���d�d�q5�i���̉\���������悤�ɍl�����܂��j�̍��v5�Ƃ������ƂɂȂ�܂��B
�@�}���K���̏ꍇ���s�Γd�q����5�ƂȂ�܂����A����͌��q�Ԋu�������傫���Ȃ邱�Ƃ���A�����͎͂キ�Ȃ�悤�ł��B
���q�Ԋu�������傫���Ȃ�̂́A4s�d�q�̓d�q�k���ł��邽�߂ƍl�����܂��B
�i�}���K���̏ꍇ�ł́A3d�d�q����4s�d�q�̕����G�l���M�[�������Ȃ�܂��B�j
�@�������A�ő�̕s�Γd�q���ƂȂ�̂̓N�����ƂȂ锤�ŁA���ꂪ�ł������͂������Ȃ�ƍl������̂ł����A���̎����ł͂��̂悤�ɂ͂Ȃ�܂���B
���̑��̌��f�ɂ����ē������ŗZ�_�E���_���ő�ƂȂ�̂́A6�����̃^���O�X�e���ƂȂ�܂��B
�܂��A����͑S���f�̒��ōő�̗Z�_�ƕ��_�������܂��B
���̕ӂ�̎���͕��G�Ȃ悤�ł��B
�@�Ȃ��A�K���E���̏ꍇ�ł́A���_�͍������̂́A�Z�_�͂��Ȃ�Ⴍ�Ȃ��Ă���̂������ł��B
����́A���������ƊW����d�q��sp2�����O���ɂȂ邽�߂ƍl�����܂��B
�܂�A����͕��ʌ^�̂��̂ł��邱�Ƃ��瓙���I�Ɍ�������̂�������߂ɁA�ő̌������ێ�����͂��ア�̂��ƍl�����܂��B
�܂��A�Q���}�j�E���̏ꍇ�ɂ́Asp3�����O���ɂȂ�悤�ŁA����͒Y�f�̏ꍇ�Ɠ������_�C�������h�^�ɂȂ�܂��B
�@�����ŁA���̂��Ƃ�������邽�߂ɁA3d�d�q��4p�O���ɏ��ʂ���ƍl���܂��B
���̌��́A���̌��q������5.5�ƂȂ�悤�ł��邱�Ƃ���2�ƂȂ�܂��B
���������āA���������ɂ����铺�̓d�q�z�u�́A���̂悤�ɕς�܂��B
3d 4s �d �d �d �d �d �E �@���@
3d 4s 4p �d �d �d �E �E �E �E �E �@
�@�������Ȃ���A����ł͓��̓��d���̍����������ł��܂���B
�Ƃ����̂́A���d���̍����͎��R�d�q�����q�ƏՓ˂����ہA�U���x�̏������ɂ���Đ��������̂ł����A���̂��Ƃ�d�d�q�k���ł��Ă��邱�Ƃɂ����̂ŁA����Ɩ������邱�ƂɂȂ�܂��B
���d���̍����́A��͂�d�d�q�k���`������A������s�d�q�ɂ���čs�Ȃ��邽�߂ƍl���A���_�̍����ɂ��ẮA���x�������Ȃ�ƁA���̓d�q�z�u����L�̂悤�ɕς邽�߁A�Ƃ������ƂŐ������邱�Ƃ��ł��܂����A���q�ԋ����̕��͐����ł��܂���B
�@���ɁA�������ς�����ꍇ�̓����ł̕ω����ǂ��Ȃ邩�Ƃ������Ƃ��^��Ƃ��Đ����܂��B
���̏ꍇ�ɂ́A����d�d�q�ł���ʎq�����傫���Ȃ邱�Ƃ���G�l���M�[�������Ȃ�A�����͂���܂�܂��B
�������A���̂��Ƃ͓������f�̏ꍇ�̂��Ƃł��B
���f���ς�ƌ��q�j�̗z�d�ׂ��ς�܂�����A��ʎq���������邱�Ƃɂ��G�l���M�[�̑��含�ƁA�z�d�ׂ������邱�Ƃɂ��G�l���M�[�̌������Ƃ����E�I�ɂȂ�܂��B
�@�܂��A���̂��Ƃɂ͕k���ł��邱�Ƃɂ�錴�q�j�̗z�d�ׂ̎Օ������W���邱�ƂɂȂ�܂��B
���̂��Ƃ������Ȃ̂��A���J�������ł�����A�܂��A���J�������̏ꍇ�ɂ͂ǂ��Ȃ邩�Ƃ������Ƃ��q�ׂ邱�Ƃɂ��܂��B
�@�܂��A�d�q�̃G�l���M�[E�͎��̂悤�ɂȂ�܂��B
�����ŁAk�͔��W���ł��B
���̎����A�G�l���M�[��Zeff/n�̓��ɔ�Ⴗ��Ƃ������ƂɂȂ�܂��B
E���|k
Zeff 2
����������
n2
�@�����ŁA���̗L���j�d�ׂ��ǂ̂悤�ɂȂ邩�Ƃ������ƂɂȂ�܂����A����Ƃ��Ă͗Ⴆ�A4s1�����J���E��(Z=19)�Ǝ��̎�����5s1�������r�W�E��(Z=37)�Ƃ��r���邱�Ƃɂ��܂��B
�@�J���E���̑��C�I�����G�l���M�[��4.34eV�ł����A���r�W�E���ł͂����4.17eV�ɂȂ�܂��B
���������āA���C�I�����G�l���M�[�̔�iRb/K�j��0.961�ɂȂ�܂��B
�@����A������(Z/n)2�̔�́A
�ƂȂ�܂��B
(37/5)2
������������
(19/4)2��2.43
�@���ꂪ�L���j�d�ׂ�p���邱�Ƃɂ���āA0.961�ɂȂ����Ƃ������Ƃł�����A"�L���j�d�W��"�i����͗L���j�d��=�W���~Z�Ƃ�����́j�̔�����Ƃ���ƁA���̊W���������܂��B
1 : a2��2.43 : 0.961
���̂悤�ɁA��r�I�傫���L���j�d�W�����������܂��B
�� a��0.63
�@�Ⴆ�A�ŊO�k�ɂ��ꂼ��4s�d�q��5s�d�q�����A��(Z=29)����(Z=47)���r����ƁA���̂悤�ɂȂ�܂��B
�����̃C�I�����G�l���M�[�́A����7.72eV�ŁA�₪7.58eV�ɂȂ�܂��B
���������āA�����̔�(Ag/Cu)�́A0.982�ɂȂ�܂��B
����A(Z/n)2�̔�́A
�ƂȂ�܂��B
�����ŁA�����̗L���j�d�W���̔�����Ƃ���ƁA���̊W���������܂��B
(47/5)2
������������
(29/4)2��1.68
1 : b2��1.68 : 0.982
���̂悤�ɁAd�d�q�ɂ��j�d�ׂ̎Օ����͎�܂��Ă��܂��B
�� b��0.76
�@���ꂪ�ǂ̒��x�ɂȂ邩�Ƃ������Ƃ��������߂ɁA�������̃J���E���Ɠ��ɂ��Ĕ�r���邱�Ƃ��܂��B
�����̃C�I�����G�l���M�[�̔�́A7.72/4.34=1.78�ɂȂ�܂��B
�܂��A(Z/n)2�̔�́A(29/4)2/(19/4)2��2.33�ɂȂ�܂��B
���������āA�����̗L���j�d�W���̔�����Ƃ���ƁA���̊W���������܂��B
1 : g2��2.33 : 1.78
���̂悤��d�d�q�k�ɂ��j�d�ׂ̎Օ��͑��Ɣ�ׂĎア���̂ƂȂ�܂��B
�� g��0.87
�@d�d�q�̏ꍇ�ɂ͂ǂ����Ă��̂悤�ȏɂȂ邩�Ƃ����A���̋O�����������Ƃɂ��ƍl�����܂��B
�܂�A���̋O��������ɂ͑����̓d�q���K�v�Ȃ��Ƃ���A���q�j�̗z�d�א������ꂾ�����������邱�ƂɂȂ邩��ł��B
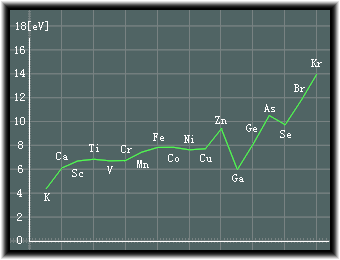
��4�����̌��f�̃C�I�����G�l���M�[
�@�������Ad�d�q�̏ꍇ�ɂ͂��܂�ω�������܂���B
���̗��R�́Ad�d�q�̏ꍇ�ɂ͂��ג����O�����Ƃ邽�߂ł��B
�܂�A���[�����q�̓����ɓ��荞�O�����Ƃ邱�ƂɂȂ�܂��B
���̂��߁A�����̓d�q�ɂ��Օ��̉e�������܂�Ȃ��Ƃ������ƂɂȂ�܂��B
�@d�d�q���d�q�k�ɂ��Օ����̉e�������������Ƃ��炩�A���̑��ɂ����Ă͌�̎����قǗZ�_�╦�_���������Ă��܂��B
�@�J�ڋ����̏ꍇ�A�ŊO�k�ɂ���d�q��d�d�q�ƂȂ�A���ꂪ���̌��q�Ƌ��L������z�ʌ������s������A���̓d�q���D���A�z�C�I���ƂȂ��ăC�I���������s�����ƂɂȂ�A���̂��`�����܂��B
�@���̂Ƃ́A���q�̌��q���Ƃ��čl��������������̌���������Ă�����̂ɑ��Č����܂��B
�@�����͓d�q����o���ėz�C�I���ɂȂ�₷�������ł��B
����A�_�͓d�q��ߑ�����\�͂����������ł�����A�_�Ƌ������q���������āA�������q�͗z�C�I�������邱�ƂɂȂ�܂��B
�z�C�I���������������q�͐��ɗn���邱�ƂɂȂ�܂��B
����͉��̏ꍇ�Ɠ��l�ł��B
�@�Ȃ��A���_�ɉߎ_�����f���܂����n�t���g�p����ƁA�قƂ�ǂ̋������n����Ƃ���܂��B
�@�����̎��C�I�����ɂ́A�傫���������������Ə펥��������܂��B
�������Ƃ����̂́A�����Ɏ�����������Ƃ��A���̎���Ɣ��Ό����Ɏ��C���[�����g�������邱�Ƃł��B
�펥���Ƃ����̂́A�t�Ɏ���̕����Ɠ������Ɏ��C���[�����g�������邱�Ƃł��B
�������͏펥���ɔ�ׂĂ��Ȃ�ア���Ƃ���A�펥��������ꍇ�ɂ͔������͕����B����Ă��܂��܂��B
�@���̎��C���[�����g�ʂ́A�������Ԃɂ��A���̂悤�ɒ�`����܂��B
���̎������Ԃ́A���q�̑S���C���[�����g��J�̓��ɔ�Ⴕ�A��Ή��x�ɔ���Ⴕ�܂��B
�܂�A���̂悤�ɂȂ�܂��B
������H
�@�펥���͓d�q�̃X�s���ɂ����̂ŁA����͕s�Γd�q������ꍇ�ɐ����܂��B
�_�f���q���펥���������̂́A�����������q�O���ɓd�q���P�������Ă��邱�Ƃɂ��܂��B
����Const�
��J2
��������
T
�@�����̏ꍇ���A�s�Γd�q������Ǝ������������ƂɂȂ�܂��B
�������A���q�O���ɂ͒Ⴂ���ʂ̂��̂���l�܂��Ă������߁A�e�G�l���M�[���ʂɂ͑œ����Ă������ƂɂȂ�܂��B
�e�G�l���M�[���ʂɑi�����j�œ������ꍇ�ɂ̓X�s����0�ƂȂ�܂�����A���q�O���ɓ������d�q�ɂ���Ă͎����������ɂ͑S���s�\���ł��B
�Ȃ��Ȃ�A���̕s�Γd�q���̍ő�l��1�ƂȂ邩��ł��B
�@���������āA�펥���͎��R�d�q�⋤�L�����ƊW���Ȃ��A���q���̕s�Γd�q�ɂ����̂ƂȂ�܂��B
�i�Ȃ��A���R�d�q�̏ꍇ���A����͌������s���Ă��Ȃ����̂ł͂Ȃ��āA�����̌��q�ƌ������s�Ȃ��Ă�����̂ł��B�j
�܂�A�����Ɍ��q���̓d�q�Ƃ��Ďc���Ă���s�Γd�q������ꍇ�Ɏ����������邱�ƂɂȂ�܂��B
�@���̂��Ƃ͋��������̏ꍇ�ɂ͉\�ɂȂ�܂��B
�Ƃ����̂́Ad�d�q�̏ꍇ�ɂ͑����̕s�Γd�q�������邱�Ƃ���A�S�Ă̌������s�Ȃ���Ƃ͌���Ȃ�����ł��B
3d 4s �d �E �E �E �E �d
3d 4s 4p �E �E �E �E �E �E �E �E �@
�@�܂��A�N��������j�b�P���܂ł̌��q���͑��6�ɂȂ�܂��B
���������āA��3d�d�q��4s�d�q����N���ĕs�Γd�q�����ő�ƂȂ�̂̓R�o���g�̏ꍇ�ƂȂ�܂����A�d�q�����������C�I���̂��̂����邽�߁A���̍ő�͓S�ƃR�o���g�̒��ԂɂȂ�܂��B
���̂悤�ɋ������̂ƂȂ�̂́A���̎����ł͓S�A�R�o���g�A�j�b�P���ɂȂ�܂��B
�@���l�̂��Ƃ́A5�����̌��f�ɂ��Ă������A���̏ꍇ�ɂ̓��e�j�E���A���W�E���A�p���W�E���ƂȂ�܂����A�����̌��f�͓S�A�R�o���g�A�j�b�P���̌��f�ɔ�ׂėy���Ɋȑ��݂ƂȂ��Ă��邱�Ƃ���A�ʏ�͏��O����܂��B
�������A�������g�p���Ă��d�����̂��ł��邾���ƂȂ�܂��B
�@�����̎����̂ł́A�e���q�̎��C���[�����g�͏���ȕ����������Ă��āA���̂܂܂ł͎����������܂���B
�������A����̒��ɒu�����ƁA�e���q������̕����������A�����������������ƂɂȂ�܂��B
���C��тт���͋������̂͏펥���������܂��B
����͊e���q���m�̃X�s���̌����������Ă���������C���[�����g�̃G�l���M�[���Ⴂ���Ƃ��A�G�l���M�[�I�Ɉ���ƂȂ邽�߂ł��B
�i���̂��߁A���C���[�����g�̌����������ƁA�]���ȃG�l���M�[���M�Ƃ��ĕ��o����܂��B�j
�������A���M�ɂ���čĂъe���C���[�����g�͏���ȕ����������悤�ɂȂ�܂��B
|
R(1)�|R(n)��0.300log10(n) | (4.2) |
|
8n8�{ 6n6��1 | (4.3) |
|
|
R(n6)�|R(n8)��1.751�|1.516��0.235��0.300{log10(n8)�|log10(n6)}��0.3log10(n8/n6) |
|
�� n8/n6��10(0.235/0.300)��6.07 |
|
8n8�{6n6��8n8�{(6/6.07)n8��1 |
|
�@�� n8��1/9.00 |
|
n6��1/(9.00�~6.07)��1/54.6 |
|
|
n8��1/9.02�C�@n6��1/53.2 |
�@���āA��������̌��q�ԋ����Ƃ��̌����\����������Ό������Ƒ�}�̌��q�������߂��܂��B
�����ŁA��Ƃ��ēS�̌��q�������߂邱�Ƃɂ��܂��B
�@�S�͑̐S�����\���������A����̓��`�E���̏ꍇ�Ɠ����ɂȂ�܂��B
�܂��A���̒P�����̌������a��1.165���ŁA���������̏ꍇ�̌��q�ԋ�����2.482���ł�����A������n�͎��̂悤�ɂȂ�܂��B
|
n��10{(1.165�|2.482/2)/0.300}��0.558 |
|
0.558�~9.00��5.02 |
|
n��10{(1.173�|2.556/2)/0.300}��0.447 |
|
0.447�~12��5.36 |
4.6 �d�C�`����
�@�����̏ꍇ�A�ő̓������R�ɉ^������d�q�����邱�Ƃɂ���āA�ő̂̂���ꏊ�Ő������d���M�G�l���M�[��`���邱�Ƃ��ł��܂��B
�����ŁA���̓d�C�d�����ɂ��ď����ڂ����q�ׂ邱�Ƃɂ��܂��B
�@�d�C��H�ɓd����������Ɠd��������A����͓d���ɔ�Ⴕ�܂��B
�d���Ƃ͒P�ʎ��ԓ���ɗA�������d�ׂɔ�Ⴕ�����̂ł��B
�܂�A1�b�Ԃ�1�N�[�����̓d�ׂ��A�������Ƃ��A���̓d���̑傫����1A�i�A���y�A�j�ƒ�`������̂ł��B
�@���āA�����̒��ł������A���̓d�C�d������M�`�����������̂ł����A����͎��̂��Ƃɂ��܂��B
���R�d�q�����������ꍇ�A�d�q���d��ɂ���ĉ�������Ă��A���q�ɏՓ˂��ēd�q�̉^���͌������邱�ƂɂȂ�܂��B
���������āA�d��ɑ���P�ʎ��ԓ���̓d�ׂ̗A���ʁA�܂�d���͖{���l������ꍇ�����������Ȃ�܂��B
�������q�Ƃ̏Փ˂ɂ��d�q�̌������������Ȃ�A�d�C�d���������܂邱�ƂɂȂ�܂��B
�@�������A�i�q���U�����āA���̈�l���z����̂��ꂪ������ƁA�U���͂��̂����2�敽�ϒl�ɔ�Ⴗ�邱�ƂɂȂ�܂��B
���̏ꍇ�ɂ�3d�O�������Ă��āA���q�Ƃ��Ă͋��Ώ̓I�ɂȂ�A��l���������Ȃ�܂��B
���̂��߁A�M�U�����s���Ă��Ă��A�����2�敽�ϒl�͏������Ȃ�ƍl�����܂��B
�@�������ł͓d�q�͔��ɍ����ɉ^�����Ă��܂����A���ꂼ�ꂪ����ȕ����ɉ^�����Ă��邱�Ƃ���A�S�̂Ƃ��Ă͓d���̗���͂Ȃ����̂ƂȂ��Ă��܂��B
�Ƃ��낪�A�O������d�ꂪ��������ƁA�e�d�q�͓d��ɂ���ĉ�������A�d��̋t�����ւ̗��ꂪ�����邱�ƂɂȂ�܂��B
�i�d�q�̗���Ɠd���̕����͋t�ɂȂ�܂��B�j
���̉����x�^���ɂ���ēd�q�̉^���G�l���M�[�͑������܂�����A�d�q�̔g����ԂƂ��ẮA���̃G�l���M�[���ʂɈڂ�K�v������܂��B
���̂悤�ȕω��͘A���I�Ȃ��̂ł�����A�G�l���M�[���ʂ��A���I�ɂȂ��Ă���K�v������܂��B
�i�Ȃ��A�d��ɂ���ĉ������ꂽ�^���͌��q�ւ̏Փ˂ɂ���Č�������܂��B�j
���̏����́A�}4.2�̂悤�ɘA���I�ƂȂ邱�Ƃ��疞������܂��B
�@���̂��Ƃ��������߂ɁA�d�q�̉^����g���̓`���Ƃ��čl������̂Ƃ��܂��B
�d�q�����q�ɏՓ˂��āA���̉^��������ς��邱�Ƃ́A�g���̓`���Ƃ��Č���ƎU���ɓ���܂��B
����ƁA���̎U�����ł��邾�����Ȃ����̂���R�����Ȃ����̂Ƃ������ƂɂȂ�܂��B
�@���̋ɒ[�ȗႪ�A���0�x�Ō����i�q���U�����Ă��Ȃ��ꍇ�ƂȂ�܂��B�i��Η�x�ł������i�q�͗�_�U�����s���Ă��܂����A���̉^���͓d�q�̉^����W���Ȃ��Ƃ���܂��B�j
���̏ꍇ�ɂ́A�d�q�̔g���͈�l�ȓd��̒���i�ނ��ƂɂȂ邽�߁A���܂͋N���Ă��U���͋N��܂���B
����͌��̏ꍇ�Ɠ��l�ł��B
�@���Ǝ����悤�Ȍ��f�Ƃ��Ă̓A���J��������A���J���y�ދ���������킯�ł����A��������r�I���d���������Ȃ��Ă��܂��B
�������A���̒��ł̓A���J�������̓��d�������܂荂���Ȃ��̂ł����A����͋��������̎コ���W���Ă���悤�ɍl�����܂��B
�܂�A�A���J�������̏ꍇ�ł͔M�U�����傫���Ȃ�Ƃ������Ƃ��W���Ă���ƍl�����܂��B
�@�A���J���y�ދ����ł́A�x�����E�����ł����d���������A����͓��Ǝ��Ă��܂��B
���ہA�Z�_�͓���1083���ł���̂ɑ��āA�x�����E����1278���ƁA���������������炢�ɂȂ��Ă��܂��B
���̂��Ƃ́A���q���m�������������Ă���Ƃ������Ƃł�����A���̋����i�q�͂��ꂾ�������ɂ������ƂɂȂ�܂��B
|
����er | (5.1) |
|
1.602�~10-19[C]�~5.29�~10-11[m]��8.47�~10-30[C�Em] |
|
1D��3.335�~10-30[C�m] |
�@���L�������Ă���q���q�̏ꍇ�A�d�C�A���x�̍����قڑo�Ɏq���[�����g(D)�ɓ������Ȃ�Ƃ���܂��B�@
5.2 �o�Ɏq-�o�Ɏq���ݍ�p
�@�o�Ɏq�ƂȂ��Ă��镪�q���m�ɂ͑o�Ɏq-�o�Ɏq���ݍ�p�������A���̂悤�ɕ��q�ԗ͂��������ƂɂȂ�܂��B
|
�@A��B�̑o�Ɏq���[�����g�����ꂼ���1�C��2�Ƃ��A�����̊Ԋu��r�Ƃ���ƁA���̑��ݍ�p�G�l���M�[E�͎��̂悤�ɂȂ�܂��B
| (5.2) |
5.3 ���f����
�@���f���_�f�⒂�f�Ȃǂ̂悤�ɓd�q����������͂��������̂Ƌ��L����������ƁA���L�����d�q�͂����̌��q�ɋ������������A���f���͗z�q���I�o�����悤�ɂȂ�܂��B
�������A���f�͍ł����������Ƃ���A���̌��q�ɏ\���ɐڋ߂��邱�Ƃ��ł��܂��B
�܂�A����͑o�Ɏq-�o�Ɏq���ݍ�p�̈��ɂȂ�܂��B
���̂��߁A���̂悤�Ȑ��f�͓d�C�A���x�̍������q�ɐڋ߂���ƁA�N�[�����͂ɂ�茋�����������܂��B
���̌����̂��Ƃ͐��f�����ƌĂ�A���̂悤�Ɏ�����܂��B
�@�d�C�A���x�̍������q�Ƃ��ẮA�t�b�f�A�_�f�A���f�A���f������܂��B
�t�b�f�̓n���Q�����f�̒��ł͍ł��������A�d�C�A���x���ł������Ȃ��Ă��܂��B
���̂��߃t�b�����f�iHF�j�͐��f�C�I������o���₷���A���̐��n�t�ł���t�b�����f�_�́A�ɂ߂Ĕ������̍����_�ƂȂ�܂��B
�Ȃ��A�t�b�f�K�X�͋ɂ߂Ĕ��������������Ƃ��猀��ɂȂ��Ă��܂��B
�@���������Đ��f�����Ƃ����̂́A�����̏ꍇ�A�_�f�ƒ��f�ɂȂ�AA��B�͂����̌��f�ƂȂ�܂��B
�d�C�A���x�͒��f�����_�f�̕����������߁A���͐��f�����̑�\�I�Ȃ��̂ƂȂ�܂��B
5.4 �t�@���f�����[���X��
�@�t�@���f�����[���X�͂́A�����̕��q���m���\���ɐڋ߂����ꍇ�Ɍ�������͂ł��B
������o�Ɏq-�o�Ɏq���ݍ�p�Ǝ����悤�Ȃ��̂ƂȂ�܂��B
�ȉ��ł́A���̗͂ɂ��Đ������邱�Ƃɂ��܂��B
�@���q���ł́A���q�͊e���L�����ɂ��e�O������������Ăقڋ���̓d�ו��z�������ƂɂȂ�܂��B
�d�_�͂�����̏�Ԃŗ��������Ă���킯�ł͂Ȃ��A�d�q���^�����Ă��邱�Ƃ����ɕϓ����Ă��܂��B
���������āA����u�ԂɌ���A�d�_�ɂ͕肪�����Ă��đo�Ɏq�ƂȂ��Ă��܂��B
�@�t�@���f�����[���X�͂��A��K�X���q���ɂ����T�O�}�Ŏ����ƁA���̂悤�ɂȂ�܂��B
�@���ɂ́A�d�ו��z���E�ɕ�Ƃ����悤�ɁA���݂ɓ������ēd�ׂ��邱�ƂɂȂ�܂��B
���̌��ʁA���q�j�̐��d�א��������I�Ɍ����āA�����̓d�_�ƐÓd�I���͂������邱�ƂɂȂ�܂��B
���������āA���q�����Ȃ��w���E����l�I���Ȃǂ̊�K�X���f���A�t�@���f�����[���X�͂ɂ�茋�����܂��B
�@�t�@���f�����[���X�͂͌��q�╪�q���傫���Ȃ�ɂ��������ċ����Ȃ�܂��B
���̗��R�́A���̗͂��d�q���i�����炭���q�j�̗z�q�����j�ƊW����悤�ɂȂ邽�߂ł��B
�܂��A���q�╪�q�̕��ɐ��Ƃ��W���܂��B
�@��K�X�△�ɐ����q�̏ꍇ�ł́A���_�̓t�@���f�����[���X�͂Ƃ����W���邱�ƂɂȂ�܂�����A���̒��̊�����ȉ��Ɏ������Ƃɂ��܂��B�i�l�͍ŐV�̂��̂Ƃ͏����قȂ�悤�ł��B�Ȃ��A���x�̒P�ʂ̓P���r�����x�ŁA�����0K=-273.15���ɂȂ�܂��B�j
�@���̕\�̂悤�ɁA�����悤�Ȃ��̂ł́A�t�@���f�����[���X�͂͂��������d�q���Ɣ�Ⴕ�Ă��܂��B
�������A�n�����قȂ�ꍇ�ɂ́A�P�d�q����̃t�@���f�����[���X�͂͂��Ȃ葊�ق�����܂��B
���̗��R�͕��ɗ����قȂ邽�߂ŁA���̕\�̕��q�͊�K�X�ɔ�ׂĕ��ɗ����傫�����Ƃ���A�t�@���f�����[���X�͂������Ȃ�܂��B
���ɗ������������̂Ƃ��ẮA��K�X�̑��ɂ͗z�C�I��������܂��B
�@�Ƃ���ŁA���q���t�@���f�����[���X���͂��ő�ƂȂ鋗����������ɐڋ߂��悤�Ƃ���ƁA�d�q�k���`�����ꂽ�d�_���m�ɂ��}���I�Ȕ����͂������A���̊k�̓����ɓ��荞�ނ��Ƃ͂ł��Ȃ��Ȃ�܂��B
���̔��a�̂��Ƃ́A���q�̃t�@���f�����[���X���a�ƌĂ�A���ꂪ���q�̎����I�ȑ傫�����߂���̂ƂȂ�܂��B
�i���̔��a�́A�C�I�����a�Ƃقړ����ɂȂ�܂��B�j
�@����̌��q�ɂ��āA���L�������a�i�P�����̏ꍇ�j�ƃt�@���f�����[���X���a�̒l�����̕\�Ɏ����܂��B
�P�ʂ́��ł��B
�@���̕\�ŁA���f�̋��L�������a�͑��̌��q�ɑ���ꍇ�̂��̂ŁA���f���m�̏ꍇ�ɂ�0.38���ɂȂ�܂��B
�܂��A�Y�f�ɂ��ẮA��d�����ƎO�d�����̏ꍇ�̋��L�������a�́A���ꂼ��0.67����0.6���ɂȂ�܂��B
�@���āA�퉷�Ńt�@���f�����[���X�͂ɂ�茋���������̂Ƃ��Ă͎��b�_������܂��B
���b�_�͕��ʒ����Y�����f�������J���{���_�ł����A����͔�ɐ������ł���Y�����f���ԂɃt�@���f�����[���X�͂������A���b�_���m�͎キ�������邱�ƂɂȂ�܂��B
����́A�u�ԓI�ȑo�Ɏq�ɂ���Ď��̂悤�Ɍ����������̂ɂȂ�܂��B
�s�O�a���b�_�̏ꍇ�ɂ́A���q���܂�Ȃ����Ă��邱�Ƃ���A���b�_���m�̐ڐG�ʐς��������Ȃ�A���������Č����͂��ቺ���܂��B
���̂��Ƃ��A�s�O�a���b�_�𑽂��܂ޖ����퉷�ʼnt�̂ƂȂ��Ă��闝�R�ł��B
�@�܂��A�������b�Ɏ��������������퉷�Ńt�@���f�����[���X�͂ɂ�茋�����Ă��܂��B
����͍זE�����`�����Ă�����̂ŁA���̒��Ŗ������̂悤�Ɍ`�����Ă��܂��B
��}�ŁA"o"�̓����_����A"�\"��2�̎��b�_��\�������̂ł��B
�����̎��b�_���m�ɂ̓t�@���f�����[���X�͂������A�������łȂ��̂ɂ��Ă��܂��B
�Ƃ����Ă��A���b�_�̈�͕s�O�a���b�_�ƂȂ��Ă��āA������x�̉���������܂��B
6. �ߎ��@
�@���q���m�̌�������舵���ɂ́A��̕��@������܂��B
��́A�����������q���m�ōl���錴�q�������@�ŁA������́A�����̌��q���ꏏ�ɂ������̂ōl���镪�q�O�����@�ł��B
�����͋ߎ��@�ł����A�ߎ��@��p������Ȃ��̂͑����̊j����ѓd�q���܂ޏꍇ�̓d�q�̋O�����V�����[�f�B���K�[�̔g���������ɂ���Đ��m�ɉ������Ƃ��ł��Ȃ����Ƃɂ��܂��B
6.1 ���q�������@
�@���q�������@��VB�iValance Bond�j�@�Ƃ��Ă�A���������q�O�����m�ł̌����ōl������̂ł��B
���������āA�d�q�͓�̌��q�̊Ԃɑ��݂��邱�ƂɂȂ�܂��B
����͏]���̂悤�Ɍ��q���m����Ō��ԍl�����̂��̂ŁA����ΕW���I�Ȍ����̂��̂ł��B
�@VB�@�ł́A�ȉ��̂��Ƃ����肵�Ă��܂��B
�@����
�@���q�������̌��q�������}�ɂ���ĕ\����鎞�i�������e���q�j�̈ʒu�͕ς��Ȃ��j�A����ɂ͋�������Ƃ����܂��B
���͈ȉ��̂悤�Ȃ��Ƃł��B
�@���ɏd�v�ȗ�Ƃ��ẮA��_���Y�fCO2������܂��B
����͏]���́A
�Ƃ����\���ōl�����Ă����̂ł����A���ۂɂ͎��̋��Ƃ��čl�����Ă��܂��B
���̂悤�ɍl�����邱�ƂɂȂ����̂́AC-O�Ԃ̋��������̓�d�����ƎO�d�����̒��Ԃ��炢�̋����ɂȂ邱�Ƃ���ł����B
�܂��A���̌����G�l���M�[�����G�l���M�[���l���Ȃ��Ƃ��܂������ł��Ȃ����Ƃ���ł��B
6.2 ���q�O���@
�@���q�������@�����q�̊e�d�q�͌��q�O���ɑ��݂��A�o���̕s�Γd�q���Ќ�����Ό��������邱�Ƃɂ���Č������Ă���ƍl����̂ɑ��āA���q�O���@�͊e�d�q�������̌��q�j�𒆐S�ɂ������q�O�������̂ƍl���܂��B
�܂�A���q�������@�ł͌����d�q�͌��̌��q�j�̕t�߂ɋǍ݂�����̂ƍl����̂ł����A���q�O���@�̏ꍇ�ł́A�����̌��q�j�̎��ӂɍL�����ĕ��z������̂ƍl���܂��B
���������āA���q�O���@�̏ꍇ�ł͋��L�d�q�͓�̌��q�̊Ԃɂ������݂�����̂Ƃ������Ƃɂ͂Ȃ�܂���B
���̂��Ƃ́A�d�q������̌��q�j�ɑ����������̂łȂ����Ƃ��l����A���R�̂��ƂƂȂ�܂��B
�d�q�͒P�ɂ��ꂪ���G�l���M�[�ɂ��������āA�|�e���V����������^��������̂ɂ����܂���B
���̂��Ƃɂ��S�炸�A���q��������Ɍ��q�������@�ōl����ꂽ��A����ŕ\�������̂́A���q�������A��d�������d�����Ȃǂ̐��ɂ���Č��q���m������ŊȒP�ɕ\���邱�Ƃɂ��܂��B
�������Ȃ���A����͕X�I�Ȃ��̂ł���A�^�̌�����Ԃ�\�������̂ł͂Ȃ����Ƃɒ��ӂ���K�v������܂��B
�@���āA���q�������@�ł́A���q�������Ќ�����Ό����ɂ��g�����̏d�Ȃ�ɂ���čl���܂����A���q�O���@�̏ꍇ�ł͂��̂悤�Ȍ����͍l���Ȃ��ŁA�P�Ɍ����O���┽�����O���Ƃ������Ƃɂ���čl���܂��B
�����O���Ƃ͌��q�j�ԋ������Z���Ȃ�ꍇ�ɃG�l���M�[���Ⴍ�Ȃ�O���̂��̂ŁA�������O���Ƃ͋t�ɂ��̋����������Ȃ�ꍇ�ɃG�l���M�[���Ⴍ�Ȃ�O���̂��Ƃł��B
���̂��Ƃ́A�d�q�̓d�_���ǂ̂悤�ɕ��z���邩�ɂ����̂ŁA���ꂪ���q�j�Ԃɍ������x�ŕ��z����Ȃ�Ό������̂��̂ƂȂ�A�t�Ɍ��q�j�Ԃł̓d�ז��x���Ⴍ�Ȃ�Ȃ�Δ��������̂��̂ƂȂ�܂��B
�����Ƃ��A�����O���ł����q�j�ԋ������Z���Ȃ肷����ƁA���q�j���m�̔����͂̕��������Ȃ邱�Ƃ���A���鋗���ȏ�ɂ͐ڋ߂��܂���B
�@���q�O����\�����@�ɂ́A�e���q�O���̈ꎟ�����i���`�����j���Ƃ���@�iLCAO�@�FLinear Combination of Atomic Orbitals�j����ʓI�ł��B
�i�Ȃ��A���q�O����p���Ȃ��ʼn�͓I�Ɏ�舵�����̂Ƃ��� Hartree-Fock�@������܂����A����͐��l��͓I�ɋ��߂邱�Ƃ���A���Ƃ��ĕ\������̂ɂ͌����Ă��܂���B�j
����͌��q�������@�ł̋��̐����\���Ɠ����ɂȂ邱�Ƃ���A���҂͓������ʂɋA�����܂��B
�@Rayleigh-Ritz�@
�@�V�����[�f�B���K�[�̔g���������́A���f���q�̏ꍇ�������đ����̕ϐ����܂ޕΔ����������ƂȂ邱�Ƃ���A�������͓I�ɉ������Ƃ͕s�\�ɂȂ�܂��B
�����ŁA����Ó��Ȋ��ɂ���ċߎ�����Ƃ������@���Ƃ��܂��B
���̏ꍇ�A�σp�����[�^���܂ނ̂���ʓI�ŁA���̒l�����肷��K�v������܂��B
���߂悤�Ƃ���g�����͕��q�������s�Ȃ��g�����ł��邱�Ƃ���A����̓G�l���M�[���Œ�ƂȂ���̂��I������邱�ƂɂȂ�܂��B
A - H �c B
�@���f�����̋�����2�`9kcal/mol���x�ŁA��ʓI�ȋ��L�����i�P�����j�̋���40�`110kcal/mol���͑啪�キ�Ȃ�܂��B
���̏ꍇ�ł́A����͖�5kcal/mol�ɂȂ�܂��B
�@���f�͌��q���a���傫�����Ƃ���A���f���������ɂ͏\���ł͂Ȃ��Ƃ���܂��B
�@�Ȃ��ADNA�̓�d�����͂��̉���m�̐��f�����ɂ���Č`������Ă��܂��B
�@���̑o�Ɏq���A���̌��q�ɏ\���ɐڋ߂���ƁA�o�Ɏq�̗U����p�������邱�ƂɂȂ�܂��B
�܂�A�ڐG�������q�̕\�ʏ�ɂ���e���q�̓d�q�Q�ɑ��Ĕ��̑o�Ɏq���ꎞ�I�ɐ��������邱�ƂɂȂ�܂��B
�@���̗͂́A�o�Ɏq-�o�Ɏq���ݍ�p������p�͂̋y�Ԕ͈͂�����ɋ����Ȃ�A����͋�����7��ɔ���Ⴕ�܂��B
�i�Ȃ��A���̌����G�l���M�[�͋�����6��ɔ���Ⴕ�܂��B�j
���������āA���̗͂͌��q�╪�q���قڐڐG�����ꍇ�ɓ������̂ƂȂ�܂��B

�@�e��K�X���f�̐����͎��Ă��邱�Ƃ���A�����̃t�@���f�����[���X�͂͌��q�ԍ��ɂ���������Ⴗ��悤�ɂȂ�܂��B
��K�X�ȊO�ł́A���ɐ��̂��̂ł���A���j�q���q�ɓ����͂��t�@���f�����[���X�͂ƂȂ�܂��B
���f �d�q�� �Z�_(K) ���q �d�q�� �Z�_(K) He 2 4.2 H2 4 20.4 Ne 10 27.2 N2 14 77.3 Ar 18 87.3 O2 16 90.2 Kr 36 119.9 F2 18 85.0 Xe 54 165.1 Cl2 34 239 Rn 86 211 Br2 70 332
�@�t�@���f�����[���X���a�́A���̐}��b�̒����ɂȂ�܂��B
�܂��A���L�������a��a�̒����ɂȂ�܂��B
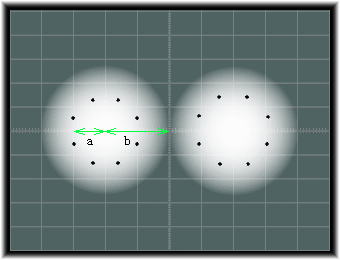
���q ���L�������a �t�@���f�����[���X���a H(���f) 0.30 1.2 C(�Y�f) 0.77 1.70(�x���[���̌����̔���) N(���f) 0.70 1.5 O(�_�f) 0.66 1.40 F(�t�b�f) 0.64 1.35 P(����) 1.10 1.9 S(����) 1.04 1.85 Cl(���f) 0.99 1.80
�@��L�̃t�@���f�����[���X���a��L.Pauling�̌��ς���ɂ����̂ł����A����͕��q�ԋ��������߂����̂ŁA���ۂ̔������Ƃ�10%�قǂ̈Ⴂ������悤�ł��B
A�F �{�|�{�|�{�|�{�| B�F �|�{�|�{�|�{�|�{
�@ �� �@ �@ o
|o
|o
|o
|o
|o
|o
|o
|o
|o
|o
|o
|o
|o
|�@ |
o|
o|
o|
o|
o|
o|
o|
o|
o|
o|
o|
o|
o|
o�@ �� �@
�@���������́A�g���O���Z���h�i�������b�j���\�����Ă���3�̎��b�_�i�G�X�e���ɂȂ������́j�̈�������_��ɒu������������̂ŁA����͋ɐ������邱�Ƃ���A�������b�Ƃ͈قȂ�e�����������܂��B
���̌��ʁA���̒��ł͒������b�̂悤�ɂ͌ł܂炸�ɉ��ɒ������сA�����`�����邱�ƂɂȂ�܂��B
�@���d�q�n���������߂ɂ͑��ϐ��̕Δ����������������K�v������܂����A����𐔊w�I�ɉ������Ƃ͔��ɍ���ɂȂ�܂��B
�Ⴆ�A����Ƃ��ėL���Ȃ��̂ɓV�̉^���ɂ�����O�̖�肪����܂��B
�@�ǂ���̕��@�����ǂ��邱�Ƃɂ���ē������ʁi�j�ԋ����⌋���G�l���M�[�j�ɓ�����A���̈Ӗ��ł͓����Ȃ��̂Ƃ���܂��B
�������A���q�������@�͌��q���m�̌�������Ō��]���̍l�����̂��̂ŁA����݂₷���Ƃ������_������܂��B
����A���q�O���@�̏ꍇ�ɂ́A���܂蒼���I�ł͂Ȃ��̂ł����A��萳���������ɓ������Ƃ������_������܂��B
�@�ʏ�́A���L�����d�q�͓�̌��q�ԂɋǍ݂���Ƃ����l���ŏ\���Ȃ̂ł����A���q�̑Ώ̐��������ꍇ�ɂ́A���ۂɂ͌����d�q������̓�̌��q�̊ԂɋǍ݂��Ȃ����Ƃ������A�{���̌����𐳂����\�����Ă��Ȃ��Ƃ������Ƃ��N����܂��B
���̂悤�ȗ�Ƃ��Ă̓x���[��������A����͓�d�����̈ʒu�ɔC�Ӑ�������܂��B
���̏ꍇ�ɂ͕����̌����\���}�̂��̂��l���A�����̂��̂����݂��Ă�����̂ƍl���܂��B
��������������Ԃ̂��Ƃ͋��ƌĂ�Ă��܂����A����͌��q�������@�ɂ�����X�I�Ȃ��̂ŁA������������Ԃ��������̂ł͂���܂���B
�@�����������邽�߂ɂ́A���̏�������������Ă���K�v������܂��B
�Ⴆ�A�A�����V����͎��̍����̂ƂȂ�B
{�ECH2��CH�\CH2�@CH2��CH�\CH�E}
�����́A�܂Ƃ߂Ď��̂悤�ɕ\�����Ƃ��ł���B
CH2 
CH2 
CH2 �_ �Q�Q�Q�Q�Q �^ �E
�@���Ƃ��ĕ\�킳����\�I�Ȃ��̂ɂ́A�x���[��������܂��B
����̓P�N���\���}�ł͎��̐}��(a)�܂���(b)�̂悤�ɕ\�킳��A���q�������@�ł͂�����Dewer�̍\���}�i����͂��܂����݂��Ȃ��A��^���Ⴂ�̂ŏȗ����܂��j�̋��Ƃ��ĕ\������܂����A���ۂ̌����́A���̃Ό������s�Ȃ��Ă���ep�d�q���x���[���̒Y�f���q�S�̂ɍL�����Ă��邱�Ƃ���A(c)�̂悤�ɂȂ�܂��B
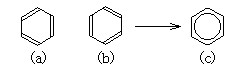
�@���Œ��ӂ���ׂ����Ƃ́A�X�̌��q���}�̍\���͉��z�I�Ȃ��̂ł����āA���ۂɂ͂����̍\���ł͑��݂��Ă��Ȃ����Ƃł��B
���ۂ̌����́A�e�\���̐��`�����i�e�\���̔g�����d�݂����ďd�ˍ��킹�����́j�ŕ\�킳��邱�ƂɂȂ�܂��B
���̂��Ƃ́A�����O���̏ꍇ�Ǝ��Ă��܂��B
�@���q�O�����́A���q�̏ꍇ�̈ꒆ�S�O�������瑽���S�O�����ɕς������̂ŁA����͌��q�O�����Ɠ����悤�ɍl���邱�Ƃ��ł��܂��B
���̕����I�Ӗ��́A���̊���2�悪�d�q�̑��݊m����^������̂ƂȂ�܂��B
���Ȃ킿��������̈�i�̐ϑf�Ёjd�тɓd�q�����������m���͂��̊���2���d�т��|�������̂ɂȂ�܂��B
�i��ʓI�ɂ͔g�����͕��f���ŕ\������܂����A���q�O�����͎����ł���Ɖ��肳��܂��B���������āA�P�ɂ���2������悢���ƂɂȂ�܂��B�j
�܂��A�e���q�O���͌������G�l���M�[�����Ƃ����̂��A���q�O���̏ꍇ�Ɠ����ł��B
�@���̍\���葱���͌��q�O���̏ꍇ�Ɠ������A���q�O���ɓd�q������ۂɂ́A�G�l���M�[�̍ł��Ⴂ���̂������Ă����܂��B
�����G�l���M�[�O���̂��̂���������ꍇ�ɂ́A�i���̑��̋O���̓d�q�Ɓj�X�s�����ɂ��ċĂ���O���ɓ���Ă����܂��B
����G�l���M�[�O���̑S�Ă��[�U�����ꍇ�ɂ́A�X�s����ɂ���2�܂œ���邱�Ƃ��ł��܂��B
�����O����2�����������邱�Ƃ́A�S�Ă̗ʎq��Ԃ�����ɂȂ���̂������邱�ƂɂȂ�A����̓p�E���̔r�������ɂ��ւ����܂��B
�@�σp�����[�^��n�ƂȂ�ꍇ�A�����̕ϐ��ɂ��G�l���M�[�u�Ȗʁv���Œ�ƂȂ�����Ƃ����̂́A�e�ϐ��ɂ��Ă̕Δ�����0�ƂȂ邱�Ƃł��B
�i���̂悤�ȕ��@�ɂ���ĉ������߂邱�Ƃ́A�ϕ��@�ƌĂ�܂��B�j
���̂��Ƃ́A1�̕ϐ��̏ꍇ�̋Ȑ����ɏ��ɂȂ�̂͂��̔����l��0�ƂȂ�A�Ƃ������ƂɑΉ����Ă��܂��B
�������A�ɑ�ɂȂ�����A�ϋȓ_�ɂȂ����肷��ꍇ������܂����A�����̏ꍇ�A�S�Ă̕Δ����l��0�̓_�Ƃ����̂̓G�l���M�[���ŏ��ɂȂ�Ƃ������Ƃ����҂ł��܂��B
�@�Ⴆ�A2�ϐ��̏ꍇ�ɂ́A���̂悤�Ȃ��Ƃł��B
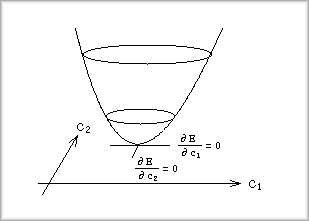
|
H����E�� |
�@H�̓n�~���g�j�A���ƌĂ�鉉�Z�q�ŁA����͗��q�̏ꍇ�ł����A���q�̉^���G�l���M�[�ƃ|�e���V�����G�l���M�[�����߂邽�߂̂��̂ł��B �܂�A����͑S�G�l���M�[�����߂邽�߂̂��̂ł��B ����́A�d�q�ɑ��ĂƂ����悤�Ɏ��ʂ̓������̂ɂ��ẮA�|�e���V�����G�l���M�[�̍��ȊO�́A�i���̕������̕\���̎d�����قȂ�ꍇ�������āj��ɓ����ɂȂ�܂��B���̎����璼�ڃG�l���M�[�����߂邱�Ƃ͂ł��Ȃ����߁A���̗��ӂɃՂ��|���Đϕ�����ƁA���̂悤�ɂȂ�܂��B
|
| (6.1) |
|
����c1��1�{c2��2�{�c�{cn��n | (6.2) |
�@LCAO�@
�@LCAO�@�͕��q�O�����iMO�j�����q�O����(AO)�̈ꎟ�����ɂ���ĕ\�킷���@�ŁA���̉�@��Rayleigh-Ritz�@�ɂ��܂��B
�@���ƂȂ�̂͌��q�O���̈ꎟ�����̑I�ѕ��ƂȂ�܂����A����͎��̏��������������悤�ɂ��܂��B
�@���āALCAO�@�ł́A���q�O���Ղ͊e���q�O����i��p���āA���̂悤�ɕ\�킳��܂��B
|
����c1��1�{c2��2�{�ccn��n | (6.3) |
�@����������є��������O�� �@���q�O��2�̈ꎟ���������2�̕��q�O���������i��ʂɂ́Ak�̌��q�O�������k�̃G�l���M�[�l�������邱�Ƃ��Ak�̕��q�O���������܂��j�A����͈�ʂɗ����q�O�������Ⴂ�G�l���M�[�̂��̂ł��錋�����O���̂��̂ƁA�����q�O�����������G�l���M�[�̂��̂ł���A�����������q�O���������܂��B ����́A���q�O���̃G�l���M�[�lE��^�������̎��̋Ȑ����A���̂悤�ɂȂ邱�Ƃ���ł��B
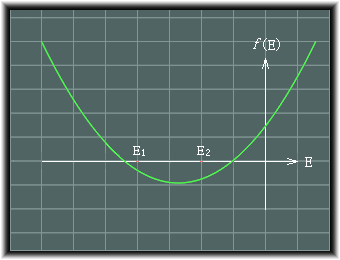
�@�������O����+����є������O����-�́A�K�i�����q�����O���āA���̂悤�ɕ\�킳��܂��B
|
��+����A�{��B | (6.4) |
|
��-����A�|��B | (6.5) |
�@���āA���������q�O�����m�̃Ќ����ƂȂ�ꍇ�ɂ́i����͌������ɑ��ĉ�]�Ώ̂ɂȂ�ꍇ�̂��Ɓj�A�������O���̓ЋO���ƕ\�킳��A���������O���̕��̓�*�O���ƕ\�킳��܂��B �܂��A2�̃��[�u�ilobe:�L����j�Ō������ăΌ����ƂȂ�ꍇ�ɂ́A�������O���̓O���ƕ\�킳��A���������O���̕��̓�*�O���ƕ\�킳��܂��B ����ɁA4�̃��[�u�Ō������ă����ƂȂ�ꍇ�ɂ́A�������O���̓O���ƕ\�킳��A���������O���̕��̓�*�O���ƕ\�킳��܂��B
�@�Ђ�Ȃǂ̂��Ƃ́A�������̒f�ʂ��猩����]���ɂ�����p�^���ʂ̗ʎq�����������̂ł��B ��ʂɁA���ꂼ��̌����ɂ�����e���q�O����p�͎��̂悤�ɂȂ�܂��B�@�܂��A�������O���Ɣ��������O����Ώ̐��̈Ⴂ�ɂ���ĕ\������ꍇ������܂��B ���̑Ώ̐��Ƃ͒��S�Ώ̐��̂��ƂŁA����_���璆�S�ɑ��Đ��������A���傤�ǔ��Α��ɂ���_�̔g�������A��Βl�������ŕ����������ɂȂ�ꍇ�]����ɑ��đΏ̂ł���Ƃ����A�܂���Βl�������ŕ��������ɂȂ�ꍇ�]����ɑ��Ĕ��Ώ̂ł���Ƃ����܂��B ���̑Ώ́A���Ώ̂̂��Ƃ́A�h�C�c���gerade�i�����́j�Aungerade�i��́j��p���ĕ\�킳��܂��B
��p��Fp(r,��)eim����Fp(r,��)(cosm���{isinm��)
�㎮�ŁAm=0�̏ꍇ���ЋO���Am=�}1�̏ꍇ���O���Am=�}2�̏ꍇ���O���ƂȂ�܂��B
�@�������̒f�ʂ��猩���ЋO���A�O���A�O���́A���ꂼ����������Ǝ��̂悤�Ȍ`�ɂȂ�܂��B
��}�͔g�����̕����݂̂��������}�ł����āA���ۂɂ�cosm�ӂ̂悤�ɓd�_�̍L���肪�ω����Ă����܂��B
�@���f���q�̌��� �@���q�����Ƃ��čł��ȒP�Ȃ��̂ł��鐅�f���q�̕��q�����ɂ��Đ������܂��B ���f���q�̌��q�O����1s�O���ł���A���̌����̓Ќ����ƂȂ邱�Ƃ���A���̌��q�O���ɂ�镪�q�O���́A�������O��1s�Ёi���邢��1�Г��j����є��������O��1s��*�i���邢��1��*���j�ƂȂ�܂��B �����̃G�l���M�[���ʂ̊W�������ƁA���̂悤�ɂȂ�܂��B
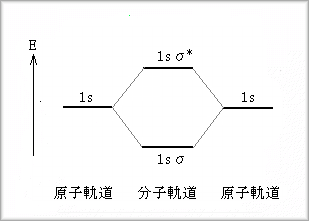
�@��L�̃G�l���M�[���ʂ̊W����A�ŏ���1s�ЋO���ɓ��邱�ƂɂȂ�܂��B
��̋O���ɂ�2�܂œ��邱�Ƃ��ł��邱�Ƃ���A�o���̌��q�̓d�q��1s�ЋO���ɓ����ēd�q�̏[�U���������A����ȕ��q�������`������܂��B
�@�Ȃ��A���q�O���𐳊m�ɕ\�킷�ɂ́A(6.4)����(6.5)���̉E�ӂɋK�i�����qN���|���邱�ƂɂȂ�܂��B ����́A��Βl�������W���ɂ�錋���̏ꍇ�ɂ͎��̂悤�ɂȂ�܂��i�Q���j�B
| (6.6) |
�@���݂��Ȃ��w���E�����q
�@�w���E���ɂ�1s�d�q��2����A�w���E�����q���m�����q��������ƂȂ�ƁA���������O����1s��*��2���邱�ƂɂȂ�A���̂��Ƃ͌������O���̃G�l���M�[�ቺ�E�������łȂ��A���q���m�̔��������N�����悤�ɂȂ�A�w���E�����q�͌`������܂���B
���̗��R�́A1s�ЋO����1s�O���Ƃ̃G�l���M�[�������A1s��*�O����1s�O���Ƃ̃G�l���M�[���̕����傫���Ȃ邱�Ƃɂ��܂��B
�܂�A���q�S�̂Ƃ��ẴG�l���M�[�̕����A���ꂼ�ꌴ�q�P�Ƃő��݂���ꍇ�̌n�̑S�G�l���M�[�����傫���Ȃ邽�߂ɁA�ʏ킱�̌����͋N����܂���B
����ł́A2s�O���ɂ��2s�Ђł͂ǂ��Ȃ邩�Ƃ����܂��ƁA�����1s��*�O�������G�l���M�[���傫���Ȃ邽�߁A���̕��q�O���ɂ͓���܂���B
�@�������A1s��*�ɓd�q��1��������Ȃ�He+�C�I���̏ꍇ�ɂ́A���̕������q���m�̏ꍇ�����G�l���M�[���Ⴍ�Ȃ邱�Ƃ���A����͒ʏ�̏������ł����݂ł��܂��B
�@�����ŁA���q�̌������̎ړx��\�킷���߂́A���������iBO:Bond Order�j�Ƃ������̂����̂悤�ɒ�`����Ă��܂��B
�@���j�q���q�̌���
�@���f���q�̏ꍇ�������G�ȓ��j�q���q�̌����ɂ��Đ����ɂ��܂��B
�x�����E���ȍ~�̌��q�̏ꍇ�ɂ́A1s�O���̑���2s�O����2p�O���Ȃǂ�����܂��B
2s�O���̏ꍇ��1s�O���̏ꍇ�Ɠ��l�ƂȂ�A�Ⴂ�̓G�l���M�[���ʂ������Ȃ邱�Ƃł��B
p�O���ɂ�錋���̏ꍇ�ɂ́A�Ќ����̑��ɃΌ������ł��܂��B
���������āA2p�O���̏ꍇ�ɂ́A�Ќ����ƃΌ����ɑ��錋�����O���Ɣ��������O���������܂��B
�@�����ŁA��������x���Ƃ���A���f���q�܂ł̏ꍇ�̕��q�O������уG�l���M�[���ʂ̊W���ȉ��Ɏ����܂��B
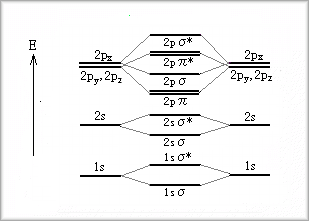
2p�O����2p�ЋO���̑��G�l���M�[���ʂ͓��j�q���q�ɂ���ĈقȂ�A���`�E�����璂�f�܂ł�2p�O���̕����Ⴂ�̂ł����A�_�f�ȏ�ł�2p�ЋO���̕����Ⴍ�Ȃ�܂��B
����́A���q�ԍ���������ɂ��������āA2p�Ђ̃G�l���M�[�̕���2p�������ΓI�ɑ傫���ቺ���Ă������߂ł��B
�@���āA���j�q���q�̏ꍇ�ɂ́A���q�O����G�l���M�[���ʂ̌��q�O�����m�̈ꎟ�����݂̂Ƃ���͉̂��̂��Ƃ������ƂɂȂ�܂����A�����1s�O���A2s�O���A2p�O���̃G�l���M�[���傫���قȂ邽�߂ł��B �������A���̂��Ƃ͈يj�q���q�̏ꍇ�ɂ͓��Ă͂܂�܂���B �Ƃ����̂́A���q���قȂ�Ɠ������q�O���ł����̃G�l���M�[���قȂ邽�߂ł��B
�@���q�O���̕\�L �@���q�O���@�̕�����ɂ����_�Ƃ��ẮA���q�O���̕\�L�ɂ��܂��܂Ȃ��̂����邱�Ƃł��B �����ŁAL�k�܂ł̓��j�q���q�̏ꍇ�̕��q�O���ɂ��Ă܂Ƃ߂����̂��A���̕\�ł��B
| ���S�L�� | 1s�� | 1s��* | 2s�� | 2s��* | 2p�� | 2p��y��2p��z | 2p��y*��2p��z* | 2p��* |
|---|---|---|---|---|---|---|---|---|
| �ʂ̕��� | 1�� | 2�� | 3�� | 4�� | 5�� | 1��y�@1��z | 2��y�@2��z | 6�� |
| �ȗ��L�� | (k)z�� | (k)y�� | z�� | y�� | x�� | w�� | v�� | u�� |
�@�ȗ��L���̓}���P���iMulliken�j�̒�Ăɂ��L�@�ŁA����͌��q�O�����قȂ�ꍇ�ɂ��p�����܂��B ���̋L�@�Œ��ӂ��ׂ����Ƃ́Az,y,x���̓G�l���M�[���ʂ��������̂ŁAx,y,z���Ƃ͉���W���Ȃ����Ƃł��B �܂��A����͊�{�I��2s��2p�O����L�k�̓d�q��Ώۂɂ������̂ŁAK�k��M�k�ɂ��ẮA"(k)"��"(m)"��O�ɂ��܂��B
�@�_�f���q�̏ꍇ
�@�_�f�ɂ�2�̕s��p�d�q�����邱�Ƃ���A�P���ɂ͂��̕��q�͎��̂悤�Ȍ����ɂȂ�ƍl�����Ă��܂����B
|
�@�Ȃ��A�_�f���q�͊����������̂ł����A����͂悭�����銈���_�f�̂��Ƃł͂���܂���B �����_�f�Ƃ͎_�f���q�ȏ�ɕs����Ŕ������̍��������̂��ƂŁA����Ƃ��Ă̓X�[�p�[�I�L�V�h�A�j�I�����W�J���i�EO2-�j�A�q�h���L�V���W�J���iHO�E�j�A�ߎ_�����f�iH2O2�j�A��d���_�f�i1O2�j�Ȃǂ�����A�_�f���q�̈ꕔ�͊����_�f�ɕς��܂��B
�@���f���q�̏ꍇ
�@���f�́A1s22s22p3�̓d�q�z�u�ƂȂ邱�Ƃ���A���f���q�̕��q�O���̓d�q�z�u�͎��̂悤�ɂȂ�܂��B
�@���������ۂɂ́A���̕��q�X�y�N�g���̉�͌��ʂɂ��A��L�̕��q�O���͐������Ȃ����Ƃ��m���Ă��܂��B ���q�X�y�N�g������́A���f���q��sp�����O���ɂ�镪�q�O�����`������Ă���ƍl�����Ă��܂��B �����̏ꍇ�A��萳�����͍����O�����܂߂����q�O�����m�̌����ɂ�镪�q�O���Ō������Ă��܂��B
�@�����O���ɂ�镪�q�O��
�@�����O���Ƃ��ẮAs�d�q��p�d�q�ɂ�鍬������\�I�ł��B
���q�̊���ԂƂ��ẮA��2s�d�q�͂��̋O���ɗ����������ƂɂȂ�܂����A���q���m����������Ƃ����ꍇ�Ȃǂɂ́A�̈��2p�O���ɗ�N���A�s�Γd�q�ƂȂ���2s�d�q��2p�d�q�������荇���č����O���ihybrid orbital�j���`�����邱�ƂɂȂ�܂��B
�@sp�����O���̈�͎��̂悤�ɂȂ�܂��B
|
��1��N(��s�{p) | (6.7) |
�@�܂��A��1�ɑ��Ď��̍����O���������܂��B
|
��2��N(s�|��p) | (6.8) |
|
|
�@�يj�q���q�̏ꍇ
�@�يj�q���q�̒P���ȗ�Ƃ��ẮA���f���t�b�f�̉������ł���t�b�����f������A���̌����ɂ��Đ������܂��B
�@���q�j���قȂ�Ɠ����`�̌��q�O���ł��G�l���M�[���قȂ邱�Ƃ���A�L���Ȉꎟ�����ƂȂ錴�q�O���Ƃ��ẮA���ɃG�l���M�[���������x�ɂȂ���̂�I�����邱�ƂɂȂ�܂��B
�����ŁA�����̌��q�̃G�l���M�[���ʁi�y�ѕ��q�O���j�������ƁA�ȉ��̂悤�ɂȂ�܂��B
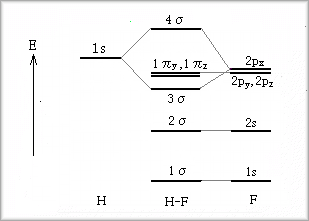
��}�̂悤�ɁA�G�l���M�[���������炢�ɂȂ�̂́A���f��1s�O���ɑ��ăt�b�f��2p�O���ƂȂ�܂��B
�������A�Ώ̐��̊ϓ_����As�O����p�O������������ɂ̓Ќ����ƂȂ�K�v������܂��B
�����ŁA���̌�������x���ɂƂ�ƁA��������p�O����2px�ƂȂ�܂��B
�t�b�f�̌������Ȃ����q�O���́A�����̌��q�O�����w�ǂ��̂܂c��܂��B
�@���������āA�t�b�����f�̊���Ԃ́A���̂悤�ɂȂ�܂��B
�@��_���Y�f�̏ꍇ
�@�يj�q���q�̑�\�I�Ȃ��̂Ƃ��Ĉ�_���Y�fCO������A����ɂ��Đ������܂��B
�Y�f�Ǝ_�f�̌��q�ԍ���2�����Ⴄ���Ƃ���A�����̌��q�O���̃G�l���M�[�͂���قǑ傫�ȈႢ�͂Ȃ����߁A�i���ߎ��Ƃ��Ắj�������q�O�����m���������邱�ƂɂȂ�ƍl���邱�Ƃ��ł��܂��B
�@���q�O���̃G�l���M�[�́i�L���j�j�d�ׂ��傫���قǃ|�e���V�����G�l���M�[���Ⴍ�Ȃ�A���������ĉ^���G�l���M�[���܂߂��S�G�l���M�[���Ⴍ�Ȃ邱�Ƃ���i����̓r���A���藝�ɂ��܂��j�A�_�f���̌��q�O���̃G�l���M�[�͒Y�f���̂��̂ɔ�ׂđS�̓I�ɉ�����܂��B
���̂悤�Ȓ������s�Ȃ�����ŁA���j�q���q�̏ꍇ�̕��q�O���̐}���l����悢���ƂɂȂ�܂��B
�@�����ŁA�o���̌��q�̊e�d�q�q�O���ɏ[�U�����Ă����A����͒��f���q�̏ꍇ�̕��q�O���̔z�u�Ɠ����ɂȂ�ACO�͎O�d�������s�Ȃ����ƂɂȂ�ƍl�����܂��B
�@����ł́A��_���Y�f�͒��f���q�ƑS�������悤�Ȃ��̂ɂȂ邩�Ƃ������ƂɂȂ�܂����A���̂悤�ɂ͂Ȃ�܂���B
���̂��Ƃ͑o���̓d�C�A���x���قȂ邱�Ƃɂ����̂ŁA�j�d�ׂ��傫���قǓd�q����������͂��������߁A�i�����k�ɑ����錴�q�ɂ��āj�_�f�̓d�C�A���x�͒Y�f���傫���Ȃ�܂��B
���̂��߁A���L�d�q�͎_�f���Ɉ��������邱�ƂɂȂ�܂��B
�@�܂��A���f���q�̏ꍇ�ɂ͓d�q1����苎��ƌ������キ�Ȃ�̂ł����A��_���Y�f�̏ꍇ�ɂ͌��������܂�܂��B ���̂��Ƃ́A���ۂɂ͎O�d�����ɂȂ��Ă��Ȃ����Ƃ��������Ă��܂��B
�@���ۂɂ͑o���̌��q�O�����m����������Ƃ������́A�����O���isp�����O���j���m�̌����ƂȂ�܂����A����͒��f���m�̂悤�ɎO�d�������邱�Ƃɂ͂Ȃ�Ȃ��悤�ł��B ���̂��Ƃ́A�ȉ��̂悤�ɐ�������܂��B
�@�܂��A�Y�f����ю_�f�ɂ��āA���ꂼ��2s�d�q1��2p�d�q1�ɂ��sp�����O�����`������A����͈�����傫���c���p�d�q�̂悤�Ȃ��̂ƂȂ�܂��B �������As�O����p�O���̍����䗦�̈Ⴂ�ɂ��A�قȂ�G�l���M�[���ʂ�sp�����O�����ł��܂��B
�@���q�O���y�э����O���ɂ���_���Y�f�̃G�l���M�[���ʂ͈ȉ��̂悤�ɂȂ�܂��B�@������sp�����O�������2p�d�q�ɂ����̂ƂȂ�܂��B sp�����O���ł́A�G�l���M�[�I�Ɏ_�f��sp�����O���̍������̂��́isp2�j�ƁA�Y�f����sp�����O���̒Ⴂ���̂��́isp1�j�Ƃ��������܂��B �������A�_�f��sp�����O���̒Ⴂ���̂��́isp1�j�ƁA�Y�f����sp�����O���̍������̂��́isp2�j�́A�����O���i��nb�j�ɂȂ�܂��B ����A�������ɑ��Đ����ȓd�_�ƂȂ��Ă���2p�d�q���m�̓G�l���M�[�I�ɋ߂����߁A�����̓Ό������邱�ƂɂȂ�܂��B
�@�d�q�̏[�U�́A�S�d�q����14�ł��邱�Ƃ���A�Y�f��sp2�ɂ���nb�܂łƂȂ�܂��B CO�ōł��G�l���M�[��������nb�͌��q�Ԃɓd�_�����Ȃ����̔��Α��ɑ������߁A����͒Y�f���q���������������ɍ�p���邱�Ƃ���A���ꂪ���苎���邱�Ƃ́A���q�ԋ�����Z�k�����ĕ��q���������߂邱�ƂɂȂ�܂��B
�@�Ȃ��A�يj�q���q�̏ꍇ�A���]�̑Ώ̒��S�������Ȃ����Ƃ���A���q�O����g-u�ŕ��ނ��邱�Ƃ͂ł��܂���B
�@��_�����f�̏ꍇ
�@��_�����fNO�́A��_���Y�f�̏ꍇ�����d�q����1�����������Ƃ���A����͔��������O����*��1���邱�ƂɂȂ�܂��B
���̂��߁A��_�����f�̌������͈�_���Y�f�̏ꍇ�����キ�Ȃ�܂����A���̂��Ƃ͔��������O���̓d�q��1�������ɂ����Ȃ����낤�Ƃ����\�z�ȏ�Ɏキ�Ȃ�܂��B
�Ƃ����̂́ANO�̌��q�ւ̉𗣃G�l���M�[��115kcal/mol�ł���̂ɑ��āACO�̕���256kcal/mol�ł���ACO�̔����ȉ��ƂȂ邩��ł��B
�@�܂��A����͈�̃��W�J���������Ƃ���A�펥���������܂��B
���W�J���Ƃ����Ă��A��ʓI�ɔ��ɒZ���ȃ��W�J���Ƃ͈قȂ�ANO�̏ꍇ�͈���Ȃ��̂ƂȂ��Ă��܂��B
���̗��R�́A���̕s�Γd�q�����q�S�̂ɂ킽�镪�q�O���ɂ��邽�߂ƍl�����Ă��܂��B
���̂��Ƃ́A�_�f���q�Ɠ��l�ł��B
7. ���w����
�@�L�@�������͋��L�������s�Ȃ��Ă��āA����͒������q�ƂȂ��Ă��܂����A���ۂɂ͕��ɂ��Ă��邱�Ƃ������A���̂��ߐÓd�I���ݍ�p�������邱�ƂɂȂ�܂��B
�܂��A�L�d�q��Ό����d�q�́A���d�ׂ��I�o���Ă��邱�Ƃ���A�d�C�A���x�̍������f��W�J���Ɣ������邱�ƂɂȂ�܂��B
���������ɐ��ɂ�锽���Ƃ��ẮA���f������_�Ɖ���ɂ�锽������\�I�ł��B
7.1 �C�I�����G�l���M�[
�@���錴�q�܂��͕��q�̒��̓d�q�i���̒��ł��ł��G�l���M�[�̍������́j�����������̂ɕK�v�ȃG�l���M�[�̂��Ƃ̓C�I�����G�l���M�[�������̓C�I�����|�e���V�����ƌĂ�܂��B
�C�I�����G�l���M�[�̕��͒ʏ�d�q�{���g(eV)�ŕ\�킳��A�C�I�����|�e���V�����̕��͒ʏ�{���g(V)�ŕ\�킳��܂��B
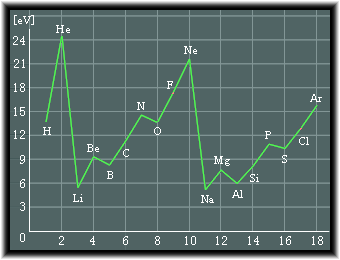
�@���f(H)����A���S��(Ar)�܂ł̃C�I�����G�l���M�[�́A���̂悤�ɂȂ�܂��B
���̐}�ʼn����͌��q�ԍ��ɂȂ�܂��B
��ʓI�ȌX���Ƃ��ẮA����̊k�̏ꍇ�A���q�ԍ���������ɂ��������ăC�I�����G�l���M�[���������Ă����܂����As�O����p�O�������S�ɏ[�U����Ă����́u�k�v���`�������Ƃ��̊k�̊O�ɂ���d�q�̃C�I�����G�l���M�[�͌������܂��B
�܂��A�_�f��C�I�E�̂悤�ɓ���O����p�d�q���ɂȂ��ē���ꍇ�ɂ��C�I�����G�l���M�[����������Ƃ����܂��B
�@
�@�܂��A���q�╪�q���m�̏Փ˂ɂ�鉻�w����������܂����A����͔M�G�l���M�[�Ƃ��čl���邱�ƂɂȂ�܂��B
�@�M�G�l���M�[��Ód�I���ݍ�p�ɂ��Ȃ������Ƃ��ẮA�d���g��d�q�̋O���J�ڂɂ�������q�̕��o�܂��͋z���ɂ����̂�����܂��B
����͌��ʎq�̃G�l���M�[�ih�ˁj�������G�l���M�[�ɂ���čl���邱�ƂɂȂ�܂��B
| (7.1) |
|
IA�| EB �� IB�| EA |
|
�� IA�{ EA �� IB�{ EB |
�������A�C�I�����G�l���M�[��d�q�e�a�͕͂��q���`�����Ă���ꍇ�ōl����K�v������A���q�ł̏ꍇ�Ƃ͈قȂ邱�Ƃɒ��ӂ���K�v������܂��B
�@����A�|�[�����O�͎��̂悤�Ɏ����܂����B
���q�̌����G�l���M�[�́A�����L�����G�l���M�[�i����͓d�q�̓d�_�������q�ɓ��������z���Ă���Ƃ����ꍇ�̋��L�����G�l���M�[�̂��Ɓj�ƃC�I�������G�l���M�[���̘a�ɂ���ĕ\�킷���Ƃ��ł��܂����A���̃C�I�������G�l���M�[�͓d�C�A���x�̑��ق��傫���قǑ������邱�ƂɂȂ�܂��B
�@�����Ń|�[�����O�́A�����L�����G�l���M�[�����ꂼ��̌��q���m�̋��L�����G�l���M�[D(A-A)��D(B-B)�̎Z�p���ςŕ\�킳���Ƃ��āAA-B���q�̌����G�l���M�[D�͎��̂悤�ɂȂ�Ɖ��肵�܂����B
|
D(A�|B)��1/2{D(A�|A)�{D(B�|B)}�{��(A�|B)�@[kcal/mol] | (7.2) |
�@�������A���f�ƃA���J�������Ƃ̌����̏ꍇ�̂悤�ɁAD(A-A)��D(B-B)�Ƃ̍����傫���ꍇ�ɂ́A���̋��L�����G�l���M�[�͎Z�p���ςł͂Ȃ��A���ςɂȂ�Ƃ���܂��B �������A���̍������܂�傫���Ȃ��ꍇ�ɂ́A�Z�p���ςƊ��ςƂ͂قړ����ɂȂ邱�Ƃ���A�ʏ�͎Z�p���ς�p���Ă���肪����܂���B�����ŁA��(A-B)�̓C�I�������G�l���M�[�ł��B ����́A�d�C�A���x�̍��ɂ���Čo���I�Ɏ��̂悤�ɊW�Â��܂����B
|
��(A�|B)��23(��A�|��B)2�@[kcal/mol] | (7.3) |
�@�|�[�����O�ɂ��A���f(H)���牖�f(Cl)�܂ł̓d�C�A���x�́A���̂悤�ɂȂ�܂��B
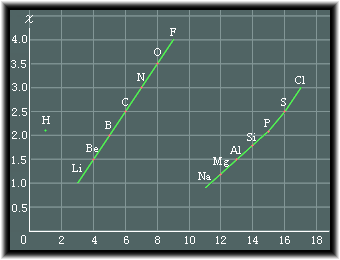
��}����A�L�@�������Ŏ�v�Ȍ��f�̓d�C�A���x�͎��̏����ɂȂ�܂��B
�@�Ȃ��A�}���P���ɂ��d�C�A���x�̒�`�Ƃ͎��̂悤�ɊW�Â����܂��B
| (7.4) |
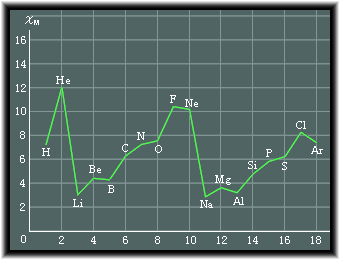
7.4 �d�q���x�ɉe�����y�ڂ����q
�@�d�q���x�ɉe�����y�ڂ����̂Ƃ��ẮA�d�q�I���ʂƗ��̓I���ʂ�����܂��B
�d�q�I���ʂɂ͗U�N���ʂƋ������ʂ�����܂��B
�@�U�N����
�@�L�@�������͒Y�f�����i�ɂ��A���w�����͐��f�̒u���ɂ��N���邱�Ƃ������Ȃ��Ă��܂��B
����͒P�����̎�v�Ȍ��f�����f�ł��邱�ƁA����ѓd�C�A���x�����܂苭���Ȃ����Ƃ��W���Ă���Ƃ����܂��B
�u�����X�e�b�h�̒�`�̂悤�ɁA�_�Ɖ���̔������v���g���̌����ɂ���Ď����꓾��̂́A���̂��߂Ƃ����܂��B
�������A���f�Ǝ������`�E���Ȃǂ̃A���J�����f������܂����A����͓d�q����o���₷�����߁A���肵�����L��������邱�Ƃ��ł��܂���B
�@�������ʁi�����ʁj
�@���q�ɂ�����d�ו��z�̕�͌��f���̓d�C�A���x�̈Ⴂ�ɂ��d�q�z�����̈Ⴂ�ɂ���Đ����邾���ł͂Ȃ��A�Γd�q�̋����n�ɂ�����d�ׂ̈ړ��ɂ���Ă������܂��B
���̋����Ƃ����̂́A���d�����ƒP�����Ƃ����݂ɕ���ł���ꍇ�̂��Ƃ������܂��B
�Ⴆ�A���̍����̂悤�Ȍ����ƂȂ��Ă���ꍇ�ł��B
���̏ꍇ�ɂ́A�d�ׂ��Γd�q�����n��ʂ��Ĉړ����邱�ƂɂȂ�܂��B
���̂悤�ɗ]���ȓd�ׁi�E���̎_�f�̂��́j���Ǎ݉������邱�Ƃɂ���ĕ��q�͈��艻���邱�ƂɂȂ�܂��B
�@���̌���
�@�_���≖��̋����́A�d�q�I���ʂ̑��ɗ��̓I�\���ɂ��e������ꍇ������܂��B
����Ƃ��Ă͗��̏�Q�����ʂŁA����͗n�}�����̏ꍇ�ł͐��f�Ƃ̔������ז�����A�����q�̐��f�Ƃ̐��f�������\���Ɍ`������Ȃ����߂ɁA����z�C�I���ƂȂ����Ƃ����ꂪ���艻���Ȃ��Ƃ������ꍇ�ɋN����܂��B
���̂��Ƃ͕��q���傫���Ȃ�����A���ݍ����悤�ɂȂ�ƋN����悤�ɂȂ�܂��B
�@���āA��ʂɒu����͒Y�f�����d�C�A���x���������Ƃ��������߁A�u����̗U�N���ʂƂ����͓̂d�q�z�����ƂȂ�܂��B
�������A�u����ɂ͖O�a�Y�����f�ɂ��A���L����̏ꍇ������A����͒Y�f���d�C�A���x�̒Ⴂ���f�Ƃ̌����ɂ��Y�f�ł̉A�d�ׂ����債�āA�d�q�������o���悤�ɂȂ�܂����A���̌��ʂ͈�ʓI�ɂ���قNj������̂ł͂���܂���B
�@�d�q�̋z�����̓Гd�q��ʂ��ē`�B���Ă����܂����A���̌��ʂ͑��₩�Ɍ������Ă����̂����ʂŁA�U�N���ʂ͋ߖT�̌��q�݂̂ɋ�������邾���ƂȂ�܂��B
�@�܂��A���̌��ʂő厖�Ȃ��Ƃ́A�U�N���ʂƂ͈قȂ�d�q�̓`�B������������ɂ������ƁA�y�ѕ��ɂ����݂ɕς�邱�Ƃł��B
|
KA �{ mH2O ® K(H2O)p+�{ A(H2O)q- |
�@�����������̊i�q�G�l���M�[�̕������a�G�l���M�[�����Ⴂ�Ȃ�A�n���ɂ���Ă��̍����G�l���M�[�ɂ��n��M�������A���n�t�̉��x�͏㏸���܂��B
�������A�i�q�G�l���M�[�̕������a�G�l���M�[���������Ȃ�A���̍����G�l���M�[��M�G�l���M�[�Ƃ��Ď��K�v������A���̗n���ɂ���ĔM�̋z�����N����A���n�t�̉��x�͒ቺ���܂��B
�@�Ⴆ�A�����i�g���E���̊i�q�G�l���M�[��180kcal/mol�ł���̂ɑ��āA���̐��a�G�l���M�[��179kcal/mol�ƂȂ邱�Ƃ���A�n���͋͂��ɋz�M���Ȃ���i�݂܂��B
�@���̂悤�Ȕ����������I�ɐi�ނ��ǂ����́A���R�G�l���M�[�ɂ���Ĕ��f����܂��B
�܂�A�����̌��ʁA���R�G�l���M�[����������Ȃ�Δ������i�ނ��ƂɂȂ�܂��B
|
G��H�|TS |
�@�ʏ�A�G���g���s�[�͉��x���ቺ������A���̂��Ïk����Ƃ����悤�ȏꍇ�Ȃǂ������āA���R�Ɍ������邱�Ƃ͂Ȃ����傷�邱�ƂɂȂ�A-TS��0�ȉ��ƂȂ�܂��B
���������āA�n�̓����G�l���M�[����������ꍇ�ɂ́A�����͎����I�ɐi�ނ��ƂɂȂ�܂����A���̂��߂ɂ͈�ʂɊ������G�l���M�[���K�v�ƂȂ�܂��B
�@�t�ɁA�n�̓����G�l���M�[����������悤�Ȕ����ł́A���̑�������₤�悤�ȋz�M���s����K�v������܂��B
�M���\���ɋz���ł��邩�ǂ����́A�n�̃G���g���s�[����щ��x�ƊW���邱�ƂɂȂ�܂��B
|
k��Ae-E/RT |
|
logk��logA�|E/RT |
�@�Ⴆ�ΓV�Ղ��g����Ƃ����ꍇ�A�g�����̉��x�������㏸�i10�����炢�j���������ł��A�_�����̗ʂ��傫���ω����邱�ƂɂȂ�܂��B ���̂��߁A�����ŗg��������ቷ�ŗg����������N�ɂ͗ǂ��Ƃ���܂��B ���邢�́A�_�����ɂ������i�I���[�u������\�I�j���g�p�����������N�ɂ͗ǂ��悤�ł��B�@
| �@(1) |
Cl2�@®�@2Cl� |
| �@(2) |
Cl��@�{�@CH4�@®�@HCl �{ CH3� |
| �@(3) |
CH3�E �{�@Cl2�@®�@CH3Cl �{ Cl� |
�@���̂��Ƃ́A�����G�l���M�[��������A���ꂾ���������������Ƃ������ƂɂȂ邩��ł��B �܂��A�����������Ƃ͕������m�̏Փ˂ɂ�����u�������Ƃ������ƂɂȂ�܂��B ���̂��Ƃ́A�������ʂ��������ɏՓ˂����ꍇ�A�Փ˂������̂͑O�̂��̂ɑ����Ďc��A�Փ˂��ꂽ���́A���̉^���G�l���M�[�Ĕ�яo�����ƂɂȂ�̂ƁA�������̂Ƃ����܂��B �������A���q���m�̏Փ˂ł͎��ۂɂ͗��q�i���q�j�j�̏Փ˂͋N��܂���A����͓d�q�̃G�l���M�[��Ԃ�ς�����̂ƂȂ�܂��B
�@���̔����ɂ���āA�ECH3�Ƃ������W�J�����ł��āA���ꂪ���f���q�Ɣ������āA
���f�̃��W�J�����ł��邱�ƂɂȂ�܂��B
���������āA�܂�(2)�̔������N�邱�ƂɂȂ�A(2)�`(3)�̔����̓��^���Ɖ��f���q���\����������ԁA�p�����邱�ƂɂȂ�܂��B
�������A���W�J�����m�������ƈ���ȕ��q�ƂȂ�A���W�J���͏��ł��āA���̘A�������͎~�ނ��ƂɂȂ�܂��B
�@�����_�� �@���W�J���̕��q�Ƃ��Ă͎_�f���q������A���ꂪ�L�@�������ƒቷ�ʼn����i�_���j���邱�Ƃ͎����_���ƌĂ�܂��B �����_���́A���A���W�J���A�����C�I���ȂǂŊJ�n����܂��B ���ɒ��˓������ł̎_���͊��������_���ƌĂ�܂��B �Ȃ��A�����_���͖����̏d���ł���A�y�C���g�̍d���ɖ𗧂���A�����̕��s��S���̘V���̌����ɂȂ��Ă��܂��B
�@�����_���ɂ����锽���͎��̂悤�ɂȂ�܂��B
| (1) |
Ra� �{ H�|R ® Ra�|H �{ R� |
| (2) |
R� �{ � O2� ® RO�|O� |
| (3) |
RO�|O� �{ H�|R ® ROOH �{ R� |
(3)�Ń��W�J��R�E���������邱�Ƃ���A(2)�ɖ߂�A�_�����p������邱�ƂɂȂ�܂��B
�@�������A�s�O�a�Y�����f�i�A���P���Ȃǁj�̏ꍇ�ɂ́A���f���u�������̂ł͂Ȃ��A��d�����̏ꏊ�֕t������悤�ɂ��Ȃ�܂��B
�@�L�@�������̎����_���́A�����ɂ���ĉߎ_�����Ȃǂ��������邱�ƂŒቺ�����邱�Ƃ��ł��܂��B
�܂��A�t�F�m�[���Ȃǂ̍R�_���܂������邱�Ƃɂ���Ă��ቺ�����邱�Ƃ��ł��܂��B�@
|
CH3�|CH��CH2�{ HI ® CH3�|CHI�|CH3 |
�@���W�J���t���@�Y�f-�Y�f��d�����ւ̕t�������̏d�v�Ȃ��̂Ƃ��ă��W�J���t��������܂��B
����͎��̂悤�Ȕ����ł��B
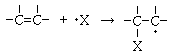
���̌��ʁA�Ăу��W�J�����������܂��B
�����ŁA���̔������N����܂��B
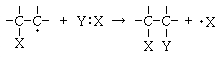
����ōŏ��̃��W�J���������A�܂������悤�ɌJ��Ԃ���邱�ƂɂȂ�܂��B
�Ȃ��A���W�J���͉ߎ_�����Ȃǂ̕����ɂ���Đ����܂��B
�@�����Y�f-�Y�f��d�����������q���\���ɂ���Ȃ�A����炪�A���I�ɏd�����邱�ƂɂȂ�܂��B
����͎��̂悤�Ȕ����ƂȂ�܂��B
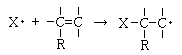
�����ŁA���̔������N����܂��B
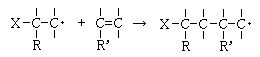
���̂悤�ɏd�����A���I�ɐi�ނ��ƂɂȂ�܂��B
���̔����̒�~�́A���W�J���Ƃ̌����ȂǁA���W�J���̐������N����Ȃ��Ȃ����ꍇ�ƂȂ�܂��B
�@�Ⴆ�A���͕s�O�a���b�_���܂ގ��b�_����\���������̂ł����A�s�O�a���b�_���\���ɑ����ꍇ�ɂ́A���W�J���ɂ���ďd�����������̂悤�ɘA���I�ɐi�ނ��ƂɂȂ�ƍl�����܂��B �i���̔����͕��G�ł��邽�߁A���m�ɂ͉𖾂���Ă��Ȃ��悤�ł��B�j
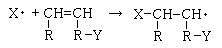
�����ŁAY�̓J���{�L�V����i-COOH�j�ł��B
����ɁA���̂悤�Ɍ������A���I�ɐi�ނ��ƂɂȂ�ƍl�����܂��B
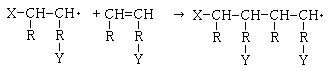
�@���̏d�����~�܂�A���̃��W�J���ƌ������Ȃ��ꍇ�ɂ́A���W�J���Ƃ��Ďc�邱�ƂɂȂ�܂��B
�Â����͎_���ɂ���ă��W�J�����c���Ă��邱�Ƃ��������߁A����ɐV�������𒍂������̂͂悭����܂���B
�@�C�I���̕t���@���W�J���̕t���ɂ��d�������Ǝ������̂Ƃ��ẮA�C�I���ɂ��ꍇ������܂��B
���̏ꍇ�ɂ́A���W�J���̂Ƃ��̕s�Γd�q�ɂ�錋���ł͂Ȃ��A�L�d�q�ɂ�錋���i�z�ʌ����j�ƂȂ�܂��B
���������āA���̔����͎_�܂��͉���ɂ���Ĉ��N������邱�ƂɂȂ�܂��B
�@�_���Y�f-�Y�f�̓�d�����ɕt�������ꍇ�A���̃Ό����̓d�q���_�ɂ���ĒD���邱�Ƃ���A���̒Y�f�̈�͐��d�ׂ������ƂɂȂ�܂��B
���̂悤�ɁA���d�ׂ����Y�f�����錴�q�c�̂��Ƃ̓J���{�j�E���C�I���ƌĂ�܂��B
����̓��W�J���Ɠ��l�ɁA�ɂ߂Ĕ������ɕx�ނ��̂ƂȂ�܂��B
�J���{�j�E���C�I���͓d�q���s�����Ă��镪�q�ł��邱�Ƃ���_�ƂȂ�A���̒Y�f-�Y�f�̓�d�������U�����ĕt�����邱�ƂɂȂ�A���l�ɏd�����i��ł������ƂɂȂ�܂��B
�@����A����Y�f-�Y�f�̓�d�������U�������ꍇ�A����̔L�d�q�ƒY�f���z�ʌ������邱�ƂɂȂ�܂��B
���̌��ʁA�Y�f-�Y�f�̓�d�����̃Γd�q�͑����̒Y�f�̕��Ɉڂ�A���̒Y�f�͉A�d�ׂ������ƂɂȂ�܂��B
���̂悤�ɁA�A�d�ׂ����Y�f�����錴�q�c�̂��Ƃ̓J���{�A�j�I���ƌĂ�܂��B
����͉���ƂȂ�̂ł�����A���l�ɒY�f-�Y�f�̓�d�������U�����āA�d�����i�ނ��ƂɂȂ�܂��B
�@�Ⴆ�A���f�C�I���i�v���g���j���G�`�����̓�d�������U�������ꍇ�A���̂悤�ɔ������i�݂܂��B
| (1) |
H+ �{ CH2��CH2 ® H:CH2�|CH2+ |
| (2) |
H:CH2�|CH2+ �{ CH2��CH2 ® H:CH2�|CH2�|CH2�|CH2+ |
|
dU��dQ�|dW | (1) |
|
dU��dQ�|pdV | (2) |
|
dU�{pdV��dQ | (3) |
|
H��U�{pV | (4) |
|
dH��dU�{pdV�{Vdp��dQ�{Vdp | (5) |
|
dS��dQ/T | (1) |
|
dS��dQ/T�@�� dQ��TdS | (2) |
�@�t�ω��ł́AdQ=TdS�ƂȂ邱�Ƃ���A������G���^���s�[��(2)���ɑ������ƁA���̊W�������܂��B
|
dU��TdS�|pdV | (3) |
�@(1)�����A���鉷�x�ɂ����ĊO������M�ʂ��ǂꂾ�����邱�Ƃ��ł��邩�Ƃ������Ƃ́A�G���g���s�[���ǂꂾ���ω��ł��邩�Ƃ������ƂƊW���܂��B
�����A���x�̈قȂ镨�����\���ɍ������ăG���g���s�[���ő�ƂȂ����ꍇ�ɂ́A�G���g���s�[�͕ω����Ȃ����ƂɂȂ�A�M�ʂ̂��Ƃ�͐����Ȃ����ƂɂȂ�܂��B
���̂悤�ɁA�O������M������ĉ��w�������i�ނ��ǂ����́A�n�̃G���g���s�[�≷�x�ƊW���邱�ƂɂȂ�܂��B
�@�Ȃ��A�O���Ƃ̔M�̂���肪�Ȃ��Ǘ��n�̏ꍇ�ɂ̓G���g���s�[�͑��傷�邱�ƂɂȂ�܂��B
�@���āA�M�͊w�����ǂ̂Ƃ��뗱�q�̉^���ɂ���Ĉ��N������錻�ۂɂ��ďq�ׂ����̂ł�����A����͗��q�̉^���ɂ������Ԗ@���ɊҌ����邱�Ƃ��ł��܂��B
�����ŁA���̊ϓ_�ɂ����Ă̓G���g���s�[�͉��ƊW���邩�Ƃ������ƂɂȂ�܂����A����̓{���c�}���ɂ���Ċm���ƊW�t�����܂����B
�@���̍l�����ɂ���ĔM�͊w����舵�����@�͓��v�͊w�ƂȂ�܂����A���v�͊w�ł̓G���g���s�[S�͎��̂悤�ɒ�`����܂��B
|
S��klogW | (4) |
| (5) |
�@���m�����͓��v�͊w�̉���ƃ����[���B���iLiouville�j�̒藝���瓱�������̂ł��B ���̒藝�́A���z���x�͈ʑ���Ԃ̋O���ɉ����ĕs�ςł���A�Ƃ������Ƃ��������̂ł��B ���̏ؖ��ɂ��ẮA�Ⴆ�Ε���16�╶��17���Q�Ƃ̂��ƁB���������āA�����I��Ԃ̐��͒P�Ɋe�v�f�ɔz�u������g���킹�̐������߂�Ƃ������ƂɂȂ�܂��B
�@���w�����̏ꍇ�ł́A�����̌��ʁA����������������ꍇ��i�^�����x�̑傫���j�C�̕��q��������ꍇ�ɂ̓G���g���s�[�����傷�邱�Ƃ���A���R�G�l���M�[���������A�����G�l���M�[�̑����������ɂ���悤�ɂ��Ȃ�܂��B
�t�ɁA�����̌��ʁA��������������ꍇ��C�̕��q��������ꍇ�ɂ́A�G���g���s�[���������邱�Ƃ���A���R�G�l���M�[�����債�A���̑��啪�ȏ�̔��M�������Ȃ��ꍇ�ɂ́A�������N����ɂ����Ȃ�܂��B
�G���g���s�[����������ꍇ�A��Ή��x�ɔ�Ⴕ�āA����ɂ�鎩�R�G�l���M�[�������Ȃ邱�Ƃ��獂���ł͔������ɂ����Ȃ�܂��B
�@�܂��A����̉���������ɂȂ�ꍇ�ɂ́A��]�̎��R�x���Ȃ��Ȃ邱�Ƃ���A�G���g���s�[���������邱�ƂɂȂ�܂��B
�������A����͕��i�^���̃G���g���s�[�Ɣ�r����Ƃ���قǑ傫�Ȃ��̂ł͂Ȃ��Ƃ���܂��B
�@��ԗʁE���x �@�M�͊w�͌����I�Ȋw��ŁA���x�͂��̏�ԗʂ̈�Ƃ��Ē�`����܂����B ���ꂪ��ԗʂł���Ƃ������Ƃ́A�n�̗����Ƃ͖��W�ł���Ƃ������ƂɂȂ�܂��B ���������āA�C�ӂ̕a�H�ɉ������ϕ���0�ƂȂ�܂��B �܂�A���̂��Ƃ��������܂��B
| (6) |
�@����A�M��Q��d��W�͏�ԗʂł͂���܂���B
�����́A�n�̗����ɂ��l���قȂ�܂��B
���������āA�a�H�ɉ������ϕ���0�ɂȂ�Ƃ͌���܂���B
�@���āA���x�Ƃ����͔̂M�͊w�I�ɓ������ꂽ��ԗʂŁA���̒�`�ɂ͔C�Ӑ�������܂����B
���̔C�Ӑ��Ƃ����̂́A���x�̋N�_�Ɩڐ��̕��ł��B
���x�̒�`�Ƃ��Ă悭�g�p�������̂ɐێ�������܂��B
����́A�X�̗Z�_�Ɛ��̕��_����Ƃ������̂ŁA�X�̗Z�_��0�x�Ƃ��A���̕��_��100�x�Ƃ�����̂ł��B
�������A���̂悤�ȉ��x�̒�`�͕��̉��x����������A�M�͊w�I�W��P���Ɏ������Ƃɂ͂Ȃ�Ȃ����߁A�s�K���Ȃ��̂ƂȂ�܂��B
�@�����ŁA�M�͊w�Ȃǂł͐�Η�x��0�x�Ƃ���A�P���r�����g�p����܂��B
����͐ێ��Ƃ͉��x�̋N�_���قȂ邾���ŁA1�x�̖ڐ��̑傫���͓����ł��B
�@���̂悤�ȑΉ��͔C�ӓI�ȉ��x�ڐ��Ƃɑ��ĉ\�ł���A�قȂ�̂̓�=0���ɑ����Ή��xT0�̒l�ł��B �܂�AQ2/Q1=T2/T1�����悤�ɁAT=f(��)���`����悢�킯�ł���A����͔C�Ӓ萔T0��p���āAT=��+T0�Ƃ��邱�Ƃ��ł��܂��B�@��L�̂悤�ɁA���x�̓}�N���I�ȏ�ԗʂƂ��Ē�`����܂������A���v�͊w�ł͉��x���`����̂ɂ��̂悤�ɞB���Ȏd�������邱�Ƃ͂ł��܂���B ���v�͊w�ł́A���x�����G���g���s�[�̕�����{�I�ȏ�ԗʂƂȂ�A���x�̓G���g���s�[�ƃG�l���M�[����A���̂悤�ɒ�`����܂��B �i�Ȃ��A�}�N���I�ɂ̓G���g���s�[�̕����B���ȏ�ԗʂƂȂ�܂��B�j
|
dS/dE��1/T | (7) |
�@���S�����E�s���S���� �@���S�����Ƃ͑S�����̂��ƂŁA�܂肠��ʂ̑S�ω���\�킷���̂ł��B �Ⴆ�Az��2�ϐ�x,y�ɂ���Ď��̂悤�ɕ\�킳���Ƃ��܂��B
|
z��f(x�Cy) |
|
�@��̎��͎��̂悤�ɐ������邱�Ƃ��ł��܂��B �C�ӂȊ��̋Ȗʂɂ����ď\���ɔ����ȗ̈���l����A���ʁi�������͒����ʁj�ƌ��Ȃ����Ƃ��ł��܂�����A���̑S�ψʂ̃x�N�g���́A�X�̍��W���ł̕ψʃx�N�g���̘a�ŕ\���邱�ƂɂȂ�܂��B�����ŁA�S����dz�����̂悤�ɏ������̂Ƃ��܂��B
|
dz��Xdx�{Ydy | (8) |
| (9) |
|
�@�t�E�s�t�ߒ�
�@�M�͊w�ł́A��ԕω��Ƃ��ĉt�ߒ��ƕs�t�ߒ��Ƃ���ʂ��܂��B
�Ǘ��n�̃G���g���s�[����������ꍇ�ɂ́A���̌������N��Ȃ����Ƃ���s�t�ߒ��ƂȂ�܂��B
�@����A�Ǘ��n�̑S�G���g���s�[�����̏ꍇ�ɂ͉t�ߒ��ƂȂ�܂��B
�i�������A�n�̌X�̃G���g���s�[�ɂ��Ă͑������邱�Ƃ��ł��܂��B�j
�O���̔M���Ւf����A�O���I�������u�������v�ƕω�����Ƃ����A�f�M�ߒ��͉t�ߒ��̈�ł��B
|
����c1��1�{c2��2 | (1) |
| (2) |
| (3) |
| (4) |
|
|
�@���ɁA(2)�̕���ł����A����͎��̂悤�ɂȂ�܂��B
| (5) |
| (6) |
| (7) |
�@(7)�̊e�p�����[�^�����肷�邽�߂ɁAE�����ꂼ��c1�Cc2�ŕΔ����������̂�0�Ƃ����A���̉i�N�������ƌĂ�鎮�������܂��B
| (8) |
|
|
|
|
�� (c1H11�{c2H12)�|(c1�{c2S12)E��0 |
�@���āA��1,��2�͋K�i������Ă���Ƃ������Ƃ���AH11�CH22�͂��ꂼ��̃G�l���M�[E1�CE2�ɓ������Ȃ�܂��B
���������āA(8)���͎��̂悤�ɏ������Ƃ��ł��܂��B
| (9) |
|
(E�|E1)(E�|E2)�|(H12�|ES12)2��0 | (10) |
�@���ɁA���j�q���q�̏ꍇ�̂悤�ɁAE1=E2�ƂȂ�ꍇ�ɂ́A���̂悤�ɂȂ�܂��B
|
(E�|E1)(E�|E1)�|(H12�|ES12)2��0 |
|
E2�|2E1E�{E12�|(E2S122�|2H12S12E�{H122)��0 |
|
�� (1�|S122)E2�|2(E1�|H12S12)E�{(E12�|H122)��0 |
|
{(1�{S12)E�|(E1�{H12)}{(1�|S12)E�|(E1�|H12)}��0 | (11) |
| (12) |
| (12') |
| E�}��E1�}�� |
�@�����̃G�l���M�[�́A����̌��q�O�����m�̌����ɂ����錋�����O���Ɣ��������O���̃G�l���M�[��^������̂ɂȂ�܂����A�d�Ȃ�ϕ��������ߎ��ł́A���������O���̕��́A�������O���̃G�l���M�[�ƌ��q�O���̃G�l���M�[���i���j�������q�O���G�l���M�[���������Ȃ�Ƃ������Ƃ������܂��B
�@���̂��Ƃ́A���q�O���̌����G�l���M�[���d�_�̕��z�݂̂ɂ���čl���邱�Ƃ��ł��Ȃ��ꍇ�ɏd�v�ƂȂ�܂��B �Ⴆ�A���������O���̓d�_�����q�Ԃɑ������z����悤�ȏꍇ�ł��B ���̂��Ƃ́A�d�_�����E�����悤�ȏd�Ȃ肪������ꍇ�ɂ́A�d�q���m�̔����͂������Ȃ邽�߂ƍl���邱�Ƃ��ł���ł��傤�B
�@���ɁA�e�W�������߂�ɂ̓G�l���M�[�̒l��(9)���ɑ������悢�̂ł����A���͂����̎��͓���̕������ƂȂ�܂��B
����͈ȉ��̂��Ƃɂ��܂��B
�@(9)�������̂悤�ȍs��A,x��p���ĕ\�������ꍇ�A
|
|
Ax��0 | (13) |
|
A-1Ax��A-10 �� x��0 | (14) |
| (15) |
�@����Ŋe�W�������߂���������������̂ŁA�����̌W�������߂�ƁA�Ⴆ��E+�ɂ��ẮA���̒l��������c1=c2�ƂȂ邱�Ƃ���A
| (16) |
| (17) |
�@�������A�d�Ȃ�ϕ�S�����ā}1/��2�Ƃ��邱�Ƃ������A����̓G�l���M�[���ʂ𑊑ΓI�Ɏ����ꍇ�ɂ͂悭�p������悤�ł��B S����r�I�傫�Ȓl�ɂȂ邱�Ƃ��炷��Ɓi�Ⴆ�A���f���q��1s�O�����m�̏d�Ȃ�ϕ���0.59�ƂȂ�A���\�傫�Ȓl�ƂȂ�܂��j�A����͑傫�Ȗ��̂悤�Ɏv���܂����A���ۂɂ͑��ΓI�ȃG�l���M�[���ʂ́AS�����Ȃ��ꍇ�Ɠ����ɂȂ邱�Ƃ������Ƃ���܂��B
�@���̂悤�ȑe���ߎ���p������̂Ƃ��āA�q���b�P���@������܂��B ����͓��ɉi�N���������ȒP�ƂȂ邱�Ƃ���悭�p������悤�ł����A�T�Z�l�����߂���A�萫�I�Ȑ���������̂ɂ͌����Ă��Ă��A���m�ȃG�l���M�[�Ȃǂ����߂�̂ɂ͌����Ă��܂���B
�@�ȏオ�A������2�̏ꍇ��Rayleigh-Ritz�@�ɂ��i�N�������̂���܂��ł����A���̂��Ƃ͊�����n�̏ꍇ�ɂ����l�ɂȂ�܂��B
���̏ꍇ�ɂ́A���̉i�N�������̍s��A�́A������i���K�i������Ă��Ȃ��ꍇ���܂߂āC���̂悤�ɂȂ�܂��B
| (18) |
| �ԍ� | ���� | ���� | ��� | �o�Ŏ� |
|---|---|---|---|---|
| 1 | ���w�����Ƃ͉��� | �Q�E�C�E�V�F�����X�L�[ | ��|�O�Y | �����}�� |
| 2 | ���q�̌`�ƍ\�� | C.A.Couslon and R.McWeeny | �猴�G���E���|�O | �������w���l |
| 3 | �N�[���\�� ���w�����_�@��2�� | C.A.Couslon | �֏W�O�E�猴�G���E��،[�� | ��g���X |
| 4 | ���q���ƕ��q�\���@����4�� | E.Cartmell and G.W.A.Fowles | �v�ۏ��� | �ۑP |
| 5 | ���w�����̊�b�@��2�� | ���ь��x | �@ | �O���o�� |
| 6 | ���w�����_�@���q�O���ƑΏ̐� | Milton Orchin, Hans H. Jaffe | �������H�i�悵�j�^�L�c�� | �{���� |
| 7 | �L�@���w�̂��߂̕��q�O���@ | M.J.S.Dewar | �猴�G�� | �������w���l |
| 8 | �\���L�@���w�i��j | Lloyd N.Ferguson | ��ؓ����E�L�c�� �⑺�G�E���䌉 | �������w���l |
| 9 | ��ʉ��w �� | L.Pauling | �֏W�O�E�猴�G���E�ˎR�Lj� | ��g���X |
| 10 | ���w�����_ | L.Pauling | ���v | �����o�� |
| 11 | �����\���E�{�C�h �L�@���w�i��A���j�@��3�� | R.T.Morrison and R.N.Boyd | �������H�E���쏹�f�E�������O | �������w���l |
| 12 | �L�@�����@�\ | Peter Sykes | �v�ۓc���u | �������w���l |
| 13 | �X���[�^�[ �t�����N�@���_�����w����@�� | John C. Slater Nathaniel H. Frank | ��㌒ | ��g���X |
| 14 | �ʎq���w�P�E�Q | P.W.Atkins | �y�����@ | �݂������[ |
| 15 | �G���g���s�[ | J.D.Fast | �s���_ | �D�w�� |
| 16 | �M�͊w����ѓ��v�͊w | A.�]���}�[�t�F���g | ���ӎq | �u�k�� |
| 17 | �����_�E-���t�V�b�c�@���v�͊w�E��@��Q�� | �G���E�����_�E �C�F�[�E���t�V�b�c | ���яH�j �� | ��g���X |
| 18 | ���q�Ɛl�� | P.W.Atkins | �猴�G���E��t�� | �������w���l |