原子軌道
1. 物質波
19世紀以前では光は波動として伝搬するというのが、従来の考え方でした。
そして、光の本性は電磁波であることが明らかになっていました。
ところが、光電効果の現象(これは、金属の表面に光を照射すると電子が飛び出す現象のことで、これは光の強さとは直接的には関係なく、光の振動数と関係します)が知られるようになると、この現象を説明するために、光は一つの粒子として物質に作用するという考えがアインシュタインによって提唱されました。
すなわち、彼によって光量子という考えが提唱されました。
しかしながら、光は干渉などの波の性質を持ちますから、これは波動でもあります。
したがって、光とは波動でもあり、粒子でもあると見なされるようになりました。
物質としては光のみが波動的性質を現わすことになったのは、この質量が非常に軽いことによります(静止質量は0)。
ところが、このことは単に相対的なものであって、全ての物質は波動性を持つということがド・ブロイによって提唱されました。
例えば、電子は回折格子によって回折現象を示し、電子は波動でもあることが実験によって明らかになりました。
したがって、物質とは粒子でもあり波動でもあるということになります。(これが原子を理解するための基本的な前提となります。)
この波動は、次の波長を持つものとなります。
ここで、λは波長、hはプランクの定数、mは質量、vは速度です。
プランクの定数はエネルギー素量を規定するものですが(このため、これに反するエネルギー状態を持つことができません)、この値は6.626×10-34[J・s]となり、非常に小さい値であるため、巨視的レベルではエネルギーは連続的であると看做すことができます。
しかし、原子レベルになると、これは有意な小ささとなり、粒子の不連続的性質が見えてくることになります。
mvは運動量と呼ばれ、pで表されます。
この場合には、ド・ブロイ波(物質波)は、次のようになります。
この関係は、次の二つの基本的な関係式から導かれました。
1.3式はプランクの式と呼ばれるもので、光のエネルギーはプランクの定数に振動数νを掛けたもの、つまりこの整数倍になるというものです。
1.4式は、相対性理論によって質量に応じてこの関係式で示されるエネルギーを持つというものです。
光の場合、光速度で運動していることより(これはどんな慣性座標系から見ても変わらないため、定まった値となります)、次の関係式を満たします。
したがって、
より
となります。
ド・ブロイは、この関係を光だけでなく、物質一般についても成立するとしたものです。
これより、1.1式が成立することになります。
1.1式より、質量の軽いものほど波動性を示すということになります。
例えば、質量9.11×10-31kgの電子の場合のh/mの値は、0.727mmとなります。
もし電子が秒速1mで運動すると、この波長の波動となりますが、普通は光速度に近いくらいの高速度で運動しています。
そこで、仮にこの速度で運動しているとすると、この電子の波長は、次の値となります。
この値はボーア半径 a0(0.53×10-10[m])に近くなっています。
このボーア半径というのは、水素の基底状態の電子(球状の電子雲となっている)が見出される確率が最も高い球面の半径のことです。
つまり、水素電子の場合、だいたいこの半径のところに電子がいるだろうという半径のことです。
そこで電子の波動を、この円周を1周期とする波(正弦波)とすれば、この波長λは
となり、この電子の速度 vは、次の値となります。
これは光速度(秒速約30万km)の0.0073倍となります。
つまり、光速度の1%くらいの速度となります。
以上のことから、電子を原子内で考える場合には、粒子ではなく、波動として考える必要が生じます。
ただし、電子は目に見えるものではないため、この挙動を知るには、このエネルギー状態の変化から生じる光を観測するということになります。
このエネルギー状態を知るには、電子は如何にあるべきかということを始めに定めることになります。
この規定が原子の現象を十分に説明できるならば、正しいと見なされることになります。
なお、光を波動と考え、電子などを粒子と考えるようになったのは、実は質量の違いによるものだったのです。
そのようなわけで、光も実は粒子ということになるのです。
(しかし、粒子概念というのは巨視的なものであって、これは仮想的なものと考えられ、物質の本質は波動と考えられます。そして粒子性は、波動同士の相互作用が起こる時、一点において生じるということから導かれるものでしょう。
このような観点は、場の量子論で指摘されています。電弱統一理論でノーベル物理学賞を受賞した一人である、S.Weibergによれば、世界は量子的場から構成され、粒子というのは相互作用する量子的場(単純には電子場、陽子場、電磁場から成る一組の場といったもの)における随伴現象にすぎない、と言っています。
例えば、光子というのは変動する電磁場のことであり、しかもこの場は量子化されている、ということです。このように波動というのは場に転換できるわけです。
つまり、ある単一の波動的存在というのは場における一つの振動ということになります。この振動は重ね合わせることができることから、振幅が等しく位相が反対のものを無から対生成できることにもなります。
しかしながら、そのような変動場では電子などの粒子の永久的存在性を説明するのが困難となりますが、実のところ永久的に存在するものはないことから(質量はエネルギーに転換されるため)、その性質は単に閉じ込められているにすぎないものと考えられます。
また、波動同士の相互作用は確率的に不作為に起こるものというよりは、自然現象を認識する者が想定するものではないかとも考えられます。
このように考えれば、「神はサイコロを振らない」筈であるというアインシュタインの考えを正当化することができます。
というのは、実際のところ物事は全く偶然的に起こるというよりは意図的に起こるようであり、しかもこのことは想定した事象が起こり易くなることからです。
この意味では、粒子的反応は単に物理現象を認識する者が想定することによって起こるものといえ、物理的機構としては本来は存在しないものと考えられます。)
ただし、光子の静止質量は0であり、何かと反応することによって、エネルギーを渡して消え去ることになります。
光が粒子または波動として存在するのは、光速度(ただしこれは媒質によって変化します)で運動する場合となります。
なお、ほとんど波動といえる光も、振動数が非常に高くなってエネルギーが非常に大きくなると、粒子性を示します。
これはコンプトン効果として知られるものです。
つまり、粒子のように物質と衝突して、この運動を変えることです。
2. 不確定性原理
不確定性原理は、ドイツの物理学者 W.ハイゼンベルグによって提示された原理で、これには位置と運動量の不確定性原理と、時間とエネルギーの不確定性原理がありますが、主に使用されるのは位置と運動量の不確定性原理となります。
位置と運動量の不確定性というのは、位置qと運動量pとを同時に正確に決定することは原理的にできないというもので、これは次のように定式化されます。
これは全体としてこのようになるということであり、例えば位置が確定している場合、pxがある確定値を持つことは可能で、この場合には他の運動量成分が不確定ということになります。
この不確定性というのは、物質が1.1式の波動性を持つことからの自然な帰結となります。
そこで、粒子を1.1式をもつ次のような波ψ(波動関数のことで、これは存在を規定するような仮想的な波となります)から成り立つものとします。
(以下のような関数はフーリエ級数と呼ばれるもので、任意の関数はフーリエ級数で表すことができます。)
| ψ= |
¥
Σ
n=1 |
Ansin2pnx/l0+Bncos2pnx/l0 |
| (2.2) |
ここで、λ0はある最大の大きさの波長とします。
もし運動量が確定したならば、λ=h/pという波長を持つ単一のsin関数もしくはcos関数となりますが、これは無限に続く波となります。
したがって、この存在確率ψ2はどこでも同じような値となり、したがって位置は全く不確定となります。
次に、2,2式の波動をある地点でのみ1となり、他は0となるような波動を考えます。
この場合には、nが1から無限大までのものが必要となります。
したがって、p=h/λから運動量pは全く不確定となります。
また、この不確定性は物質波をスリットを通過させることによっても説明できます。
物質波も光と似たように振舞い、幅の狭いスリットを通過させると回折を起すようになります。
これとしては、電子波の回折実験があります。
そこで、次のように、運動量pをもつ物質波を、幅Δqをもつスリットを通過させます。
スリットの場所では、物質波の位置はΔqだけの不確定さを持ち、回折されることによって縦方向の運動量がΔpだけ増加しますが、これは回折角θによって次のように表されます。
ところで、回折角θは
となることが知られていて、これから
となります。
つまり、位置と運動量の「誤差」の積はプランクの定数程度となります。
このようなことを厳密に表現したものが、2.1式です。
3. 電子の波動
電子とは粒子でもあり、波動でもあるということですが、この波動とは何かということが疑問として生じます。
電子は粒子でもありますから、これを観測した場合には、一点に現われることになります。
ところが、二つのスリットを通過させてどこに現われるかということを実験すると、両方のスリットを通過したかのように、波動としての干渉が起ります。
この意味では、電子は恰も二つに分裂したかのようですが、電子を粒子とみなした場合、一つの電子が分裂する筈はなく、その現象は電子が波動として伝播したことによるとしか考えられません。
そのように観測する場合(相互作用する場合)には電子は粒子として現われるのですが、その実際の挙動は波動ということになります。
この波動ですが、観測した場合には一点に現われるということですから、これは存在性の波動と考えることができます。
そして、存在性としては存在性が増えていく場合と減少していく場合の二つの変化があり、これはある振幅値を持って振動するということになります。
しかし、その結果、存在性が負になるということにもなりますが、存在性が負であるというのはおかしなことです。
そこで、この波動を二乗したものが存在確率を表すものというように定義されます。
実際、そのような操作とぴったりと合っていることから、物質の波動とはそのようなもののようです。
そうした波動を表す波動関数には複素数も使用することができます。
この場合の確率を求める操作は、波動関数を単純に二乗するのではなく、共役複素数(これはa+ibという値に対して、a-ibとなります)を掛けるということになります。
つまり、確率pは次のようになります。
これは、関数値に対する複素ベクトルの二乗ということになります。
このようにすると、虚数の値も考慮した上での実数値が得られます。
このように、波動関数を二乗した確率分布は電子雲のようなものと考えることができます。
なお、複素数を用いることができるのは波動関数に対してだけであって(このように実在の挙動を表すものが、架空的な複素数で表されるというのは実に奇妙なことといえます。むしろ、架空的なものの方が「実在」で、一方の実在というのはこの影のようなものかもしれません。実際、実在の背景にあるものの方がこの挙動をよく現し得ているようです)、実際に観測される量に複素数は生じ得ません。
例えば、2+3iというようなエネルギーはありません。
さて、波動ですから、これは重ね合わせることができます。
(これが波動を取り扱う際の要点となります。)
数学的には、これは一次結合(線形結合)と呼ばれるもので表すことができます。
つまり、次のように表されます。
ここで注意すべきことは、弦は上下に振動しますが、この運動方向は特に意味がないように、波動関数の符号も特に意味がないことです。
山とか谷とかは他方に対するものとなり、これらは同等なものです。
ただ、符号が異なるものを重ねると、波動を弱めることになるという違いがあるだけです。
4. シュレーディンガーの波動方程式
電子の簡単な波動として、原子の周りを回転する一次元の波を考えます。
ただし、波が継続的に存在するためには、定常波である必要があります。
というのは、もし定常波でないと、元に戻ってきた場合に波が干渉して弱めあうということになるからです。
(進行波の場合には、この制限はありません。)
波が定常波であるというのは、電子が永続的に存在していることからの必然的な要請となります。
この定常波の波長λは、円周をn分割とすることから、次のようになります。
さて、波長λの定常波ψは次のように表されます。
ψ=Asin(2px/l)cos(2pnt)
| (4.2) |
これは次のようにして示すことができます。
まず、一次元の波は次のようになります。
この波が速度vで進む時、t秒後には次のように変ります。
ここで、λν=vですから、上式は次のようになります。
この波が右端の固定点で反射されると、次の波に変ります。
そこで、これらの波を重ね合わせると、次のようになります。
| y+y' |
| =Asin2p(x/l-nt)+Asin2p(x/l+nt) |
|
|
|
| |
このように、定常波は空間に関する関数と時間に関する関数との積となります。
ある時間を考えれば、時間に関する値は定数となり、これは波動の形を全体的に変えるものにすぎないのですから、これは波動の原形を考える上では無視して考えることができます。
一般に運動方程式などは偏微分方程式で表現されることになるものですが、関数が各座標変数の関数の積で表されるならば、偏微分方程式は該当変数の関数についてのみ考えればよく、したがってそれは個々の常微分方程式を解くことに帰着できます。
そこで、波動関数ψは次のようにします。
これは時間を含まない場合の波動になりますが、時間を含んだものを表す場合には、波動関数をψの大文字Ψで表します。
さて、sin関数は2回微分すると、元の形と「同型」になることから、次の関係が成立します。
ただし、係数aは次のものになります。
なお、粒子の場合のこの操作は加速度を求めるということであり、これは運動方程式を求める際に行なわれます。
波動の場合には、この形を連続的に変化させるものという条件がつきますから、2回微分したものは元の関数と形が相似するものということになります。
このような関数の代表的なものとしては、他にcos関数や指数関数があります。
以上のことから、定常波というのは4.5式の関係を満たし、波に関係した固有な値aを持つものということになります。
この係数aの値は粒子の運動エネルギーEと関係づけることができ、これは次のようになります。
まず、pl=hより
| 1/l2= |
1
─────
(h/p)2 |
=p2/h2 |
| |
となります。また、p=mvより
となることより、aの値は次のようになります。
a=-(2p/l)2=-4p2・2mE/h2=-8p2mE/h2
| (4.7) |
したがって、4.5式は次のようになります。
ここで、h=h/2πとしたもの(エイチバーといわれるもの。本来はバーがもう少し上につく)を用いると、次のようにすっきりした形となります。
4.8b式は一次元の波動の場合となりますが、これを3次元の場合に拡張すれば、空間的な定常波を求めることができます。
3次元の波動に適用するには、個々の変数の偏微分で表します。
(偏微分とは、ある変数に対する微分ということになります。変数が一つの場合には普通の微分になります。)
これは、次のように置き換えることになります。
d2
───
dx2 |
® |
¶2
───
¶x2 |
+ |
¶2
───
¶y2 |
+ |
¶2
───
¶z2 |
| |
しかし、このように書くのは面倒なので、普通は上記の微分演算子を表す∇2(ラプラシアン)を用います。
これを用いると、3次元の場合には次のようになります。
あるいは、次のようにも書けます。
これは、粒子の運動エネルギーと似ています。
というのは、この運動エネルギーEは、次のようになるからです。
| E= |
1
──
2 |
mv2= |
1
──
2m |
p2= |
1
──
2m |
(px2+ py2+ pz2) |
| |
こうした対応性は一般的に成立するようで、古典力学での粒子として成立する式をシュレーディンガーの波動方程式 に置き換える際には、次の変換を行うことになります。
| px® |
h
──
i |
¶
──
¶x |
, py® |
h
──
i |
¶
──
¶y |
, pz® |
h
──
i |
¶
──
¶z |
|
| |
下にiがつくのは、これを二乗すると-1となることによります。上につけても同じ結果になりますが、下の場合には(1/i=i/i2 =)-iとなる点が異なります。
一方、エネルギーについては時間を含んだ波動関数を用いることになりますが、4.2式を時間について微分すると、ちょうど振動数νが現われて、これをエネルギーと関係づけることができます。
ただし、cosを微分すると、-sinとなり、これでは波動が変ってしまいます。
そこで、時間に関する関数はcosあるいはsinの代りに、複素指数関数を用いることになります。
つまり、次のような関数を用います。
exp(-2pint)=cos(2pnt)-isin(2pnt)
| |
この左辺を時間 tで微分すると、-2πiνがでてくる以外は同じになります。
そこで、hν=Eより、この微分係数が Eとなるようにするためには、ih/2πを掛けることになります。
つまり、エネルギーEを出す場合には、次のようにすることになります。
| E → |
ih
──
2p |
¶
──
¶t |
=ih |
¶
──
¶t |
| |
したがって、4.9a式は次のように書かれることになります。
本来は、波動関数は時間を含めたもので表すべきですが、時間微分がない場合には、時間に関する関数は単なる係数となり、これは両辺に現われますから、約されて消えることになります。
4.9式は随分面倒な式だと思われるかもしれませんが、実際にはこれを解くことはあまりなくて(最も簡単な水素原子の場合でも、これを解くのはかなり面倒になります)、大抵の人にとってはいわば概念的なもので、通常は波動関数の由来を知ったり、この結果より考えるということになります。
もちろん、簡単なものに対しては実際に適用することもできます。
この式は直交座標系の場合となりますが、一般的な座標系に対しても適用できます。
例えば、極座標系に対しても適用することができます。
この場合には、偏微分(作用素)の座標変換を行うことになります。
特に原子軌道を求める場合には球対称的となることから、極座標系を用いて解くことになります。
さて、4.9式は外場が働いていない場合の式です。
実際には、電子は原子核からのクーロン力(静電的引力)を受けて運動していますから、ポテンシャルエネルギーを考慮する必要があります。
4.9式のエネルギーというのは運動エネルギーTのことですから、これは全エネルギーEからポテンシャルエネルギーVを引いたものとなります。
つまり、実際には次の式となります。
∇2ψ=-(2m/h2)(E-V)ψ
| (4.10) |
または、次のように書かれます。
また、次のようにも書かれます。
さらには、次のように、4.11式の左辺のψにかかる演算子をまとめたハミルトニアンHで表すこともよくあります。
古典力学でのハミルトニアンの意味は、運動エネルギーTとポテンシャルエネルギーVの和ですから、この表現は自然なものです。
これらの式のことは、シュレーディンガーの波動方程式と呼ばれます。
この名は、ド・ブロイの考えを元にしてこの方程式を考え出した、オーストリアの物理学者 E.シュレーディンガーに因みます。
これ以前には量子力学の原型ともいえる、行列力学がありました。
ある場合には、こちらの方が考えやすいため、これを用いることもありますが、原子軌道や分子軌道を考える際には、シュレーディンガーの波動方程式を用いることになります。
この理由は、こちらの方が行列力学を用いて解くよりも簡単なためです。
ボーアなどは行列力学の陣営でしたから、波動力学派とは対立していました。
しかし、正しいのであればやはり物事はより簡単な方に向くことになり、量子力学といえば波動力学が主流を占めるようになりました。
もっともこれらは単に形式上の違いであって、本質的には同等のものとされます。
したがって、より原理的な行列力学から量子力学を解説するということもよくあります。
一方、原子同士の結合を考えるには、波動力学が向いています。
このため、化学結合を考える場合には、シュレーディンガーの波動方程式を用いることになります。
しかし、電子の運動を考えるには、粒子的な見方の方が簡単です。
ところでポテンシャルエネルギーの意味ですが、これは位置エネルギーのことです。
つまり、中心力場内を運動しているという場合には、位置エネルギーを持つことになります。
例えば、高い所から石を転がして、これが徐々に速度を増していくようになるのは、(エネルギーの変化として考えた場合)最初の位置エネルギーが低下していくことによるものです。
そのように物体の全エネルギーというのは、運動エネルギーと位置エネルギーの総和になります。
ポテンシャルエネルギーは、ある地点から別の地点に移動させたときの力の総和として求められます。
そこで、この力fを、
とすると(ここで、kは距離に依存しない力の係数とします)、ポテンシャルエネルギーVは次のようになります。
| V= |
ò |
f(r)dr |
= |
ò |
|
=- |
k
──
r |
+C |
| |
ポテンシャルエネルギーVは無限遠で0とするものですから、この積分定数Cは0になります。
したがって、これは次のようになります。
もし中心までの距離に比して、移動した距離が十分に短い場合には、位置エネルギーの増加はfΔrとなることが示せます。
これは、次のようになります。
| DV |
| =V(r+Dr)-V(r)=- |
k
────
r+Dr |
+ |
k
──
r |
|
|
| =- |
k
──
r |
( |
1
──────
1+Dr/r |
-1 |
) |
≒- |
k
──
r |
(1-Dr/r-1)=(k/r2)Dr=fDr |
|
| |
例えば、力が地球重力の場合、この引力は質量mに重力加速度gを掛けたものになりますから、位置エネルギーの増加分は、よく知られているようにmgΔhとなります。
ということで、ポテンシャルエネルギーVが 4.15式になるということが納得されたかと思われます。
そこで電子に働く力ですが、原子番号をZとすると、原子核の電荷はZeとなりますから、この引力fは次のようになります。(単位系はMKSA系とします。)
なお、CGSG系では、次のようになります。
このように係数までも変ってくるのは、MKSA系とCGS系とでは、電荷の取り決め方が異なるためです(主値が全く異なります)。
本によって様々となりますから、このところは混乱しがちになります。
4.16a式のポテンシャルエネルギーを用いて、4.12式を表すと、次のようになります。
| ∇2ψ+ |
2m
───
h2 |
( |
E+ |
Ze2
────
4pe0r |
) |
ψ=0 |
| (4.17) |
ところで、全エネルギーEの値ですが、これは
となりますが、ポテンシャル・エネルギーは負の値で、運動エネルギーの方は正の値です。
そこで、この総和がどうなるかということになりますが、ちょうど電子が原子内から離れて無限遠で速度が0になったとすると、運動エネルギーは0、ポテンシャル・エネルギーも0となりますから、全エネルギーはこのときに0となります。
したがって、電子が原子核に捕捉されて運動する場合には負の値となり、原子から飛び出す場合には正の値となります。
ということで、4.17式の解ですが、これは一般に次のようになるとされます。
Eが正の場合には、Eは任意な値を取ることができますが、Eが負の場合には、任意な値をとることはできず、離散した特殊な値だけとなります。
これは、まさしくボーアが言った原子の状態と一致し、シュレーディンガーの波動方程式によっても原子の状態を正しく表しています。
しかも、こちらの方はシュレーディンガーの波動方程式以外何も仮定していないという意味で、より優れた理論ということになります。
(ただし、例外はスピンになります。しかし、これは容易に決められることより問題がありません。)
5. 量子数
電子は原子内ではある決ったエネルギーで運動することより、特定の軌道を運動することになります。
この運動は一般に楕円軌道となります。
楕円軌道は、軌道面の角度と、楕円の短軸の長さ及び長軸の長さによって決ります。
これらは任意な値をとることはできず、ある値を係数とする整数値をとることになります。
また、軌道面の角度に対応するものが、磁気量子数mとなります。
軌道はこれらの量子数によって定まりますが、電子そのものの磁気量子数ともいえるスピンもあります。
主量子数は、電子のエネルギーを規定するものとなります。
(ただし、実際には後に述べる方位量子数なども関係することになります。)
これはボーアによって、電子が原子内を円運動するとき、角運動量Mは次の値にならなければならないとして導入されたものです。
角運動量は動径に対して垂直方向(つまり回転方向となります)の運動量に半径を掛けたものです。
これは、角速度ωに慣性モーメントIを掛けた量のことです。
これらは次のようになります。
多粒子系の場合には、Iは次のようになります。
粒子が円運動する場合には、
となることから、角運動量Mは次のようになります。
これは次のようになります。
ここで、×は動径ベクトルと速度ベクトルとの外積のことで、つまり動径ベクトルと速度ベクトルによって張られる平面において、動径ベクトルに対する垂直方向の成分との積を求めるということになります。
円運動する場合には、運動方向は動径ベクトルに対して垂直方向となりますから、単純に掛ければよいことになります。
したがって、5.1式は次のものになります。
これはボーアの量子条件と呼ばれるものです。
これが発表された時点では唐突な仮定でしたが、物質には1.1式の物質波を持つということからは自然に導かれます。
これは、5.1式のλに1.1式から得られるλの式を代入すればよいことになります。
つまり、次のようになります。
| nl= |
nh
──
p |
=2pr ∴ mrv= |
nh
───
2p |
| |
ボーアが何故このような仮設を持ち出したのかということになりますが、これは水素原子から放出されるスペクトルを説明するためのものでした。
つまり、このスペクトルは光の波長毎の輝線の分布ですが、これは飛び飛びになっていて、これを説明するためでした。
このことは、次のようにします。
光は振動数に応じたエネルギーを持っていますから、波長が分かればこのエネルギーが分かります。
また、原子模型は、ラザフォードによって中心に原子核があり、この周りを電子が運動しているということが実験で確かめられました。
したがって、電子が原子核の周りを回転運動し、ある軌道から別の軌道に移った際に、この差分のエネルギーが放出されればよい、と考えられることになります。
このためには、この半径が分かればよいのです。
というのは、この半径が分かればポテンシャルエネルギーが分かり、そして円運動に対する運動エネルギーも定まるからです。(5.4式より、これはポテンシャルエネルギーの絶対値の半分になります。)
5.2式には、未知変数が2つありますから、これらの変数の値を決めるためには、もう一つの式が必要となります。
これは、クーロン力と遠心力が釣り合うということから得られます。
遠心力は、mv2/rという値になりますから、次の式が成立します。
| k |
Ze2
──
r2 |
= |
mv2
───
r |
(k=1/4pe0) |
| (5.3) |
このvに5.3式から得られるvの式を代入すれば、次のようになります。
| r= |
n2h2
─────
kmZe2 |
= |
4pe0n2h2
────────
4p2mZe2 |
= |
e0n2h2
─────
pmZe2 |
| (5.5a) |
ここで、Z=1の水素原子について、n=1に対する半径を求めると、これは0.529×10-10[m]となって、ボーア半径a0と一致します。
したがって、次のように表すこともできます。
実際には、核の陽電荷は電子によって遮蔽されます。
このため、Zは有効核電荷を用いることになります。
さて、全エネルギーEはT+Vですから、まずVから示すことにします。これは次のものになります。
| V=-kZe2・ |
1
──
r |
=-kZe2・ |
pmZe2
─────
e0n2h2 |
=- |
mZ2e4
──────
4e02n2h2 |
| (5.6) |
次に運動エネルギーTは、mv2/2ですから、これは5.4式から
となります。したがって、全エネルギーEは
となります。そこで、量子数nに対するエネルギーをEnとすると、これは次のものとなります。
| En=V/2=- |
me4
──────
8e02h2 |
・ |
Z2
──
n2 |
| (5.9) |
なお、これは円軌道だけでなく、楕円軌道の場合にも成立します(実際には、少し値が異なりますが)。
上式から、エネルギーは1/n2に比例して上がっていくことになります。
この値はだいたい次のように小さくなっていきます。
1,0.25,0.11,0.06,0.04,…
電子軌道の半径が離散値を取ることから、全エネルギーも離散値となり、軌道遷移によるエネルギーの放出あるいは吸収は離散値をとることになります。
電子の安定性が原子や分子の安定性につながり、最外殻の電子における上位のエネルギー順位差が大きいものほど安定ということになり、これは最外殻の電子の主量子数が1~3までのものということになるようです。
電子の状態遷移が5.9式に従うことは、次のような実験によって証明されました。
原子に電子を衝突させると、この電子のエネルギーが、状態遷移エネルギーよりも大きい場合に限り励起が起こり、衝突した電子ではこのエネルギーに等しい分のエネルギー損失が生じることになりました。
これはFranck-Hertzの実験によります。
単原子の電子が励起されると、この状態は不安定であることから、すぐに元の状態に戻ることになり、このときにこの遷移エネルギー分のエネルギー(固有の振動数となる)を持つ光子が放出されます。
分子の場合には、単に遷移するというだけでなく、結合状態が変化するということにもなります。
なお、単原子の気体となる原子としてはヘリウム(He)やネオン(Ne)、アルゴン(Ar)、クリプトン(Kr)などがあります。
ネオンサインはネオンなどの励起によって生じる光子の放出を利用したものです。
また、気体分子の水素(H2)、酸素(O2)、窒素(N2)、二酸化炭素(CO2)もその目的に利用されます。
これらの発光色は、次のようになります。
He:黄色,Ne:赤橙色,Ar:赤色~青色,Kr:黄緑色,H2:バラ色(淡紅色),O2:オレンジ色(橙色),N2:黄色,CO2:白色。
方位量子数は副量子数とも呼ばれるもので、これは角運動量を与えるものとなります。
電子が円運動する場合には、これは主量子数と一致します。
また、これは楕円軌道の扁平率と関係した量子数で、これは楕円の短軸に対する尺度を表すものとなります。
長軸の長さの尺度は主量子数nとなることから、短軸の長さの尺度はn,n-1,…,2,1となりますが、これから1引いたものが、方位量子数 lとなります。
つまり、これは次の値となります。
主量子数nが2の場合には、方位量子数 lは1と0となります。
これが0の場合が円運動に対応するs軌道となり、1の場合が(1:2の)楕円軌道に対応するp軌道となります。
方位量子数は、5.1式のボーアの量子条件を次のように一般化したものから出てきたものです。
ここで、qiは一般化された座標系の位置変数で、piはこの位置変数に対する運動量となります。
また、積分は閉径路について行います。
なお、これはサークル積分と呼ばれるものです。
座標系には直交座標系や極座標系、円筒座標系など様々なものがあり、これらの座標系毎に座標変数とこれに対する運動量が規定されます。
角運動量を求めるには、極座標系を用いるのがよく、この場合の座標変数としては半径r、回転角φなどがあり、角運動量に対する座標変数は回転角φとなります。
したがって、これに対しては次の式となります。
ここで、閉径路は楕円軌道となり、したがって回転角については0から2πまで積分することになります。
円運動する場合には、角運動量Mは不変ですから、これは定数となってこの積分は2πMとなり、5.1式が得られます。
このように、5.1式ではなぜ2πで割ったのかということが、自然に出てきます。
このn'が方位量子数または副量子数と呼ばれるもので、普通これはkで表されます。
電子が円運動する場合には、方位量子数は主量子数と一致します。
これらが一致する理由は、主量子数というのは方位量子数を含んだものとなることによります。
kと似たものが lであり、これは
とするものです。
(このような方位量子数の定義は定義的だけでなく概念的にもかなり混乱してしまいますが。)
しかし、実際の角運動量Mはkよりもlに近くなります。
すなわち、角運動量Mは、厳密には次のようになります。
例えば、k=1に対しては Mは 0になります。また、k=100に対しては M≒99.4987となり、やはりkよりはlに近くなります。
特に、k=1の場合には、角運動量はlでの値となることから、方位量子数は lを用いることになります。
しかし、lでは方位量子数がどのようにして現われてきたものなのかが明確になりません。
さて、角度の他には動径変数 rもあり、これに対しては次のようになります。
円運動する場合には、prは0であり、rの変化もないことより、この場合には0となります。
したがって、この量子数は0以上の整数をとることになります。
主量子数nは、これらの量子数を用いて、次のようになります。
このように、方位量子数kとは主量子数から径線量子数を引いたものということになります。
そこで、nとkとの関係ですが、これは楕円の長軸の長さをa、短軸の長さをbとすると、次のようになります。
磁気量子数 主量子数と方位量子数が楕円軌道の形を決めるものに対して、磁気量子数はある軸(これはz軸とします)への角運動量成分を決めるものとなります。
つまり、これは角運動量ベクトル(回転面に対して垂直方向のベクトルになります)のz軸への射影となります。
これも量子化されて、任意の値を持つことはできず、これは次の値になります。
これより、磁気量子数mは、2l+1個の値を持つことになります。
例えば、方位量子数 1のp電子の場合には -1,0,1という値をとります。
したがって、p軌道の場合には、3個の軌道があることになります。
磁気量子数で注意するべきことは、これは本来の方位量子数kの絶対値に一致することがないことです。
というのは、もしmがkまたは-kとなった場合には(正確には kではなく、5.13式の右辺のhの係数となりますが)、このことはz軸に重なったということですから、他の成分は0となり、運動量が確定してしまいます。
しかし、このことは電子の位置が全く不確定になるということであり、これは電子がほぼ原子内にあるということと矛盾します。
しかしながら、磁気量子数を定めるz軸の取り決め方は任意的ですから、磁気量子数mがkまたは-kに一致するということにもなります。
この矛盾を解消するものが一様な磁場です。
これは、以下のことによります。
電子は電荷を持つことから、これが運動することにより、この周りに回転磁場ができます。
(この回転方向は右ネジの法則によって定められますが、電子は負電荷なのでこの反対となります。)
このため、電子が回転すると、この回転面の鉛直方向に電子による磁場が発生し、磁気双極子として働くことになります。
これが外部磁場と相互作用することになり、電子のエネルギーの増加または減少を引起こすことになります。
これはzeeman効果として知られるものです。
zeeman効果
zeeman効果についていうために、磁場Hの中を回転する電子の場合を考えます。
まず、負電荷の電子が原子核の回りを円運動するという場合、この回転によって生じる磁気双極子の磁気モーメントμは次のようになります。
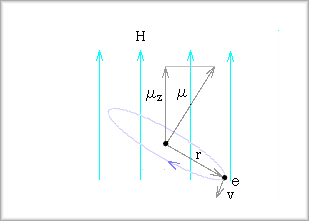
この磁気モーメントμの値は次のようになります。
ここで、μ0は真空の透磁率で、磁気モーメントのことではありません。
これが運動量pと逆向きとなるのは、負電荷のためです。
(なお、電流とは電子の運動によって生じる電荷の流れのことですが、これは正電荷を考えたものです。)
CGS単位系では、上式は次のようになります。
ここで、cで割ることの意味が不明と思われるでしょうから少し説明しますと、SI(MKSA)単位系での電荷の単位とCGS単位系での電荷の単位の決め方が全く異なっていて、SI単位系の素電荷の値をCGS単位系の素電荷の値に変換するには、10cを掛ける必要があります。
また、MKSA単位系でも磁気モーメントの定義の仕方には2種類あり、これを
とする場合もあります。
つまり、μとμ'には次の関係があります。
現在は、μ'を磁気モーメントの定義とするようです。
電子の角運動量Mはmrvとなり、また磁気モーメントは負電荷の電子の角運動量の向きとは逆になることから、これは次のようになります。
ただし、磁場Hと相互作用するのはこれと同方向の成分ですから、実際には磁場に平行な成分であるMzをとることになります。
もし電子の回転面が磁場(z軸)に垂直でない場合には、角運動量のz軸成分Mzをとれば同じことになるため、Mの代りにこのMzを用いることにします。
さて、磁場の中では、磁気双極子は-μHのエネルギーΔWを持つことから、これは次のようになります。
したがって、磁場の中ではこのエネルギーが付加することになり、電子から放出される電磁波のスペクトルが分裂することになります。
つまり、磁場がない場合のエネルギーをW0とすると、磁場H内でのエネルギーはWは、次のように分裂することになります。
ただし、この分裂にはさらにスピンも関係することになりますが。
スピン 方位量子数 lや磁気量子数 mが電子の回転運動に起因した軌道角運動量を示すものであるのに対して、スピンは電子そのものに付随する角運動量を示すものとなります。
電子の軌道は量子数n,l,mによって定まり、当初はこれで十分と思われましたが、磁気量子数による電子のエネルギー順位の分裂が、これだけでは説明できないことが分かりました。
例えば、s電子の場合、磁気量子数は0ですから、これはスペクトルの分裂を引起こさない筈なのですが、実際には磁場の中では二つに分裂します。
そこで、ある方位量子数 lが関係すると考えられることになるのですが、この場合には分裂数は2l+1となりますから、2という偶数に分裂することが説明できません。
そこで、半整数スピンなるものが考えられました。
これは、1/2または-1/2という量子数をもつものです。
これは磁気量子数mと同じように磁気モーメントを持ちますが、スピンの磁気モーメントの場合には、量子数 mの磁気モーメントの2倍になるという点が異なります。
スピンという考えが提出された当初では、これはある大きさを持つ電子が自転するというイメージのものでしたが、実際には電子が自転することによって生じているわけではありません。
スピンもまた軌道(オービタル)であり、電子が固定のスピンを持っているというわけではありません。
このため、同一軌道にはスピン軌道も付随することになり、これは値として2つあることから、Pauliの排他原理より(パウリはドイツの天才的物理学者。量子力学草創期の指導的科学者の一人で、舌鋒鋭い批判をよく行ったことから物理学者達に恐れられた。彼の書いた量子力学の本は名著とされる)、同一軌道には電子が2つまで入ることができます。
同一エネルギー順位の軌道が複数ある場合、電子はこれらの空いている軌道から詰まっていくことになりますが、これらの軌道に一個ずつ入っている電子のスピンは同方向を向きます。
このことは、スピンという小さな磁石が同方向に並ぶからという理由によるものではなく、電子の交換相互作用によるとされます。
電子の交換といったことが生じるのは、量子数が全て同じになる場合、電子同士は区別がつかなくなることから、交換可能となることによります。
反磁性・常磁性
磁場がかけられた場合、Faradayの誘導法則にしたがって誘導電流が生じ、これによって磁場の向きと反対方向の磁気モーメントが発生します。
このようなことは反磁性と呼ばれます。
原子の中の電子の場合には、誘導電流は軌道角運動量ベクトルl(正確にはこれにスピン角運動量を合成したものとなりますが)の才差運動として生じることになります。
これはLarmorの才差運動と呼ばれているものです。
この結果、次のように磁気モーメントμが発生します(電子は負電荷のため、角運動量の向きとは逆向きに発生します)。
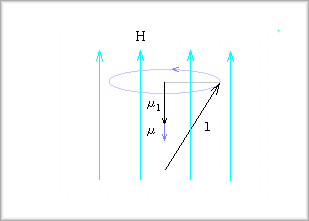
この図で、μlは軌道角運動量ベクトルlによる磁気モーメントの、磁場Hに対する成分です。
なお、lが才差運動するということは、電子の軌道面(lに対して垂直な面)が回転することを意味しています。
しかしながら、スピンは電子自身に付随したものですから、これに誘導電流が生じるということはありません。
したがって、スピンに対しては反磁性は生じません。
磁気モーメントμは、才差運動の角速度の大きさに比例することになります。
これは非常に小さいため、個々には無視されますが、物質全体としてはある大きさを持つことになります。
一方、μlの方は元々ある磁気モーメントであり、これは磁場の方向を向くことになります。
このようなことは常磁性と呼ばれます。
この図では、これとは逆の状態となっています。
また、スピンの場合も、この角運動量によって磁気双極子ができていますから、磁場と平行になります。
スピンに対しては常磁性が現われるのみとなり、これが物質の常磁性を決めるものとなります。
さて、原子は通常複数の電子から構成されていて、しかもこれらの電子は相互作用しているため、事情は複雑になります。
この相互作用(カップリング)は静電的斥力と角運動量に起因する磁気モーメントになります。
特に主量子数が同じ場合に強くなります。
そこで、実際には個々の電子について考えるのではなく、これらの電子の合成軌道角運動量Lで考えることになります。
このことは、個々の電子の軌道運動量は相互作用により才差運動を行うことになりますが、合成軌道角運動量Lの方は大きさ及び方向が一定に保たれるからです。
また、電子にはスピンによる角運動量もありますから、Lに合成スピンSを結合した全角運動量Jで考えることになります。
結局、原子の反磁性や常磁性は、原子の角運動量といえる全角運動量Jによって考えることになります。
電子の全角運動量は軌道角運動量とスピンを結合したものとなり(ただしこれは絶対値となります)、これは小文字のjで表されます。
一方、大文字のJは各電子の全角運動量を合成したもので、これはLとSとをベクトル的に加算したものになります。
しかし、このときに問題となるのが、スピンの量子数による磁気モーメントは、軌道角運動量の量子数による磁気モーメントの2倍になるということです。
このため、Jのみによっては磁気モーメントを表すことができません。
そこで、Landeのg因子と呼ばれるものが使用されます。
これは、LとSの存在比のようなもので、LjとSjをベクトルJに対する各成分であるとすると、
となりますが、gはこれらを用いて
とするものです。
もし、JがLのみの場合には、gは1となり、JがSのみの場合には、gは2となります。
角運動量は正確には量子数LやSなどではなく、{L(L+1)}1/2や{S(S+1)}1/2などに比例するもので、Jの磁気モーメントを求める因子であるgも正確にはこれらを用いて表されます。
これはLandeのg公式と呼ばれるもので、上式とはだいぶ形式が異なりますが、同じことを表したものです。
このgを用いると、Jに対する磁気モーメントμは、次のようになります。
これは、ボーア磁子μBを用いて、次のように表すことができます。
あるいは、μ'=μ/μ0,μB'=μB/μ0を用いて
となります。
現在では、ボーア磁子はμB'の方を用いるようです。
このように、電磁気学は単位系によって式が異なるため、ややこしくなっています。
古い文献を読む場合には、このことに注意する必要があります。
なお、共有結合によって結合している有機化合物の場合、大抵は全ての電子が対電子となり、したがって全スピンは0になります(この例外としては酸素分子があります)。
また、合成軌道角運動量も0となりますから、これは反磁性のものとなります。
金属の場合には、鉄やニッケルなどのように不対電子を持つものは0以外のスピンSを持ち、このような金属は常磁性を示すことになります。
6. 電子の軌道
量子数を考える上では、電子は粒子として楕円軌道を描くという描像が簡単ですが、電子による結合(共有結合と呼ばれるもの)を考えるには、電子の波動関数によって考えることになります。
これはシュレーディンガーの波動方程式を解いて得られるものです。
また、電子の存在性を考えるには、波動関数による確率分布であるところの電子雲(電荷雲)によって考えることになります。
この確率分布は、波動関数の値を二乗することによって得られます。
さて電子の軌道の大凡の形は、主に方位量子数によって決まります。
主量子数はエネルギー順位に大きく関与しますが、波動の形としては動径方向(r方向)の振動的変化と関係するようになります。
方位量子数 lの値によって、0のものがs電子、1のものがp電子、2のものがd電子などとなります。
d電子以降になると、形が少し複雑になります。
d電子はM殻以降に現われ、これはカルシウムの次の元素であるスカンジウム以降の原子に現われます。
有機化合物を構成する原子はほとんど第3周期までの原子となるため、有機化合物について考える場合には d電子以降はあまり重要ではありません。
特に有機化合物を構成するほとんどの分子は、第2周期までの原子になることから、重要な軌道は1s軌道、2s軌道、2p軌道となります。
これらの軌道(波動関数)の形は、次のようになります。

ここで、白は+の位相、青は-の位相を表します。
しかし、重要なのは値の絶対値であり、正・負の位相は本質的には同じものです。
この位相の相異は重ね合わせる場合にのみ関係することになります。
つまり、同相の場合には波動が大きくなり、位相が異なる場合には波動が小さくなります。
s軌道は球状であり、方向性を持たないため、同じ順位の軌道は一つだけになります。
p電子は亜鈴型をしたもので、これは方向性を持ち、同じ順位の軌道には三方向のものがあります(これは磁気量子数として 0,-1,1の3つがあることによります)。
これらは2px,2py,2pzとなります。
s軌道は、主量子数の違いによって、1s軌道、2s軌道などがあります。
p軌道では主量子数は2以上からとなり、これは2p軌道、3p軌道などとなります。
s軌道関数 s軌道は球対称であることから、半径のみの関数によって表すことができます。
1s軌道では、この波動関数は次のようになります。
ここで、N1sは規格化因子を表すものとします。
これは、波動関数を二乗したものを全空間に渡って積分したとき、1となるようにするための定数です。
(というのは、電子は1個しかないからです。)
この軌道の図は次のようになります。
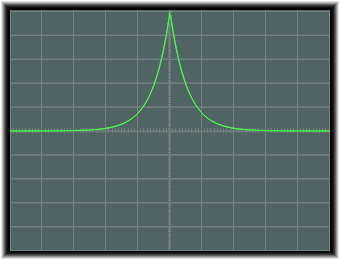
これは、原点でC1sとなり、原点から離れるにしたがって、指数関数的に減少していくものとなります。
1/aは半径相当の定数で、これはボーア半径a0を有効電荷で割ったものとなります。
有効電荷は遮蔽効果により、外側の電子になるほど小さくなります。
2s軌道では、この波動関数は次のようになります。
ψ2s=N2s・(2-ra)exp(-ra/2)
| (6.2a) |
また、これに-1を掛けたものも解となることから、次のように表すこともできます。
ψ2s'=N2s・(ra-2)exp(-ra/2)
| (6.2b) |
このことは、簡単には次のようにして証明できます。
まず、ψが次のシュレーディンガーの方程式を満たすものとします。
この両辺に-1を掛けると、ハミルトニンHは線形演算子であることから、次のようになります。
つまり、-ψも解となります。
また、意味があるのはこの二乗となる確率ですから、この意味でも符号を変えても問題がありません。
こちらの方が、内側が負になり、外側が正となることから、波動を重ね合わせる場合には考えやすくなったりします。
2s軌道の図は次のようになります。
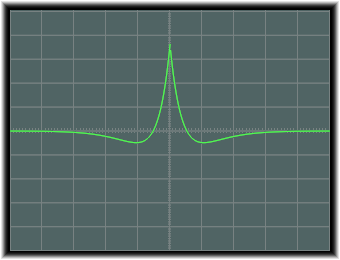
なお、exp(-ra/2)について説明すると、これは1s軌道の場合よりも指数関数の変数値が小さくなっていることから、この減少の仕方は緩やかとなり、したがって波動は広がります。
p軌道関数 p軌道は、s軌道をある軸方向に伸ばした形のものとなります。
このような変換を行うためには、ある軸の変数による関数を掛ければよいことになります。
このような関数としては、
が挙げられ、実際にこれがその関数となります。
この関数はxが大きくなると、s軌道の絶対値を大きくすることになります。
つまり、波動はより広がることになります。
ただし、この広がりはx軸の近傍でのみ大きくなります。
このことはs軌道の波動関数が半径の増大と共に減少することが関係しています。
つまり、x軸のある値のところで、x軸に垂直な断面を考えます。
この平面上では掛ける値(xのこと)が同じになるのですが、原点からの距離が最も小さくなるのは、x軸上の点となることから、この点においてs軌道の値が最も大きいということになります。
上記のことを図で示すと、次のようになります。
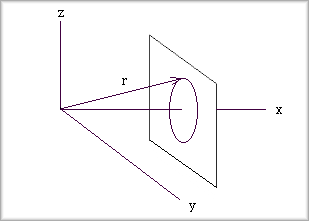
このことは y軸、z軸の場合も同様になりますから、p軌道はそれぞれ次のように表すことができます。
そこで、例えば2pxの軌道は、次のようになります。
ψ2px=N2p・xexp(-ra/2)
| (6.3) |
この軌道のx軸上での値は次のようになります。
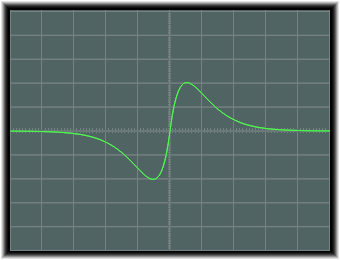
d軌道関数 d軌道は、四葉線の形をしたものが4種と、これとは別の形のもの一種からなります。
d軌道が5種必要なのは、この方位量子数 lが2であることから、磁気量子数が5種存在することによります。
d軌道は、p軌道よりも周波数の高い波動であることから、角方向での分割はp軌道よりも一つ増えることになります。
p軌道の場合には球体を1分割したものとなりますが、d軌道は球体を2分割することになり、これは四葉線のようなものとなります。
この分割方向としては、xy平面についていうと、次の二つがあります。
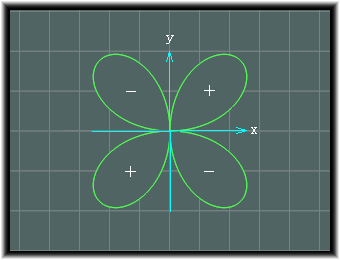
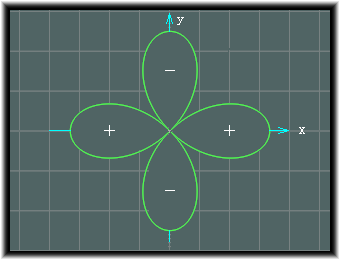
上の画像のものは、dxyと名付けられ、下の画像のものはdx2-y2と名付けられます。
このことは、これらのd軌道がそれぞれ次のように表されることによります。
ψ(dx2-y2 )=(x2-y2)¦(r)
| (6.5) |
ここで、¦(r)は、動径 rの適当な関数です。
dxyについては、y=xまたはy=-xという直線方向で最大となることは、以下のようにして示すことができます。
まず、半径rの円上について考えます。
この半径上では¦(r)の値は同じになりますから、xyの値がこの円上でどうなるかを考えればよいことになります。
そこで、この円上の点が原点となす角をφとすると、x,yは次のように表すことができます。
したがって、2xyは次のようになります。
sin2φが最大となるのはφが45゜,135°等の場合となりますから、ちょうどこの波動関数の向きになります。
xyの値は、半径を1とした場合、次の四葉線を表す式と一致します。
つまり、rに対するものが 2xyの値ということであって、この値は四葉線の図形に対応しています。
dx2-y2について、同様に求めると、次のようになります。
x2- y2=r2(cos2φ-sin2φ)=r2(2cos2φ-1)=r2cos2φ
| |
cos2φが最大となるのはφが0゜,90゜等の場合となりますから、ちょうどx軸やy軸の方向となります。
x2-y2の値は、半径を1とした場合、次の四葉線を表す式と一致します。
これらの関数は、yz平面およびzx平面についても同様ですから、それぞれ3種あります。
さて、d軌道を表すのに6種のものが考えられるのですが、d軌道には5種しかないことから、これら全てが独立しているわけではないことを示唆しています。
実際、この組合せは、dx2-y2、dy2-z2、dz2-x2の3種となります。
というのは、これらは次の関係を満たすからです。
dx2-y2+dy2-z2+dz2-x2=(x2-y2)¦(r)+(y2-z2)¦(r)+(z2-x2)¦(r)=0
| |
したがって、これらの内少なくとも一つは独立的ではないことを示しています。
というのは、一つは他の二つによって表されるからです。
そこで、これらの内一つはdx2-y2を取ります。
もう一つはdy2-z2とdz2-x2で表すことを考えます。
既に、これらの和は0となってしまいましたから、これは除外されます。
すると、次に容易に考えられるのはこの差を取ることであり、これは次のようになります。
|
|
|
|
| ={3z2-(x2+y2+z2)}¦(r)=(3z2-r2)¦(r) |
|
| (4.6) |
これがdz2となります。
ただし、規格化因子は除外してあります。
なお、dx2-y2との規格性を合わせるために、1/√3で割りますが、規格化因子は除外したことから、これは省略しました。
dz2は、次の図形をz軸の周りに回転させたものとなります。
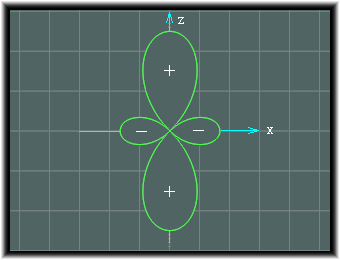
この波動関数は、pz波動関数の中央部にドーナッツの輪を嵌めたような形となり、他とはかなり変わった形となりますが、この出自を考えると、納得されることと思われます。
なお、実際の3d軌道の波動関数は、4.4~4.6の各式に規格因子N3dを掛けたものとなります。
ここで、d軌道の分類について述べておきます。
d軌道は、座標軸方向に張り出したものと、座標軸の間に張り出したものとに分けることができます。
(この座標軸というのは、実質的にはp軌道によって定まるものです。また、z軸は磁場がある場合には、この方向にとられます。)
前者の軌道は、dx2-y2とdz2となり、eg軌道と呼ばれます。
後者の軌道は、残りのdxy,dyz,dzxとなり、これはt2g軌道と呼ばれます。
これらの波動関数は、極座標を用いても表現できます。
そこで、dx2-y2について、この表示を示すことにします。
まず、極座標では、各座標値は次のように示されます。
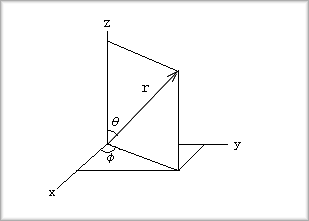
これより、各座標値は次のように表されます。
x=rsinθcosφ
| |
y=rsinθsinφ
| |
z=rcosθ
| |
このx,yを4.5式に代入すると、dx2-y2は次のようになります。(ただし規格因子は除外してあります。)
¦(r)(x2- y2) =r2¦(r)sin2θ・(cos2φ -sin2φ)=r2¦(r) sin2θ cos2φ
| (6.7) |
また、4.6式は次のようになります。
|
|
| =r2¦(r){2cos2θ-(sin2θ・cos2φ+sin2θsin2φ)} |
|
|
|
|
|
| (6.8) |
このようにこちらはφの変数を含んでいません。
したがって、dx2-y2とdz2を掛けたものを全空間について積分すると、
| ò ò ò |
G(r,θ)cos2φdrdθdφ |
= |
ò ò |
G(r,θ)drdθ |
ò |
2p
0 |
cos2φdφ |
=0 |
| |
となり、これらが直交することが示されます。
ここで、G(r,θ)はdx2-y2とdz2を掛けたものに対する rとθに関する関数です。
実際には、これらのd軌道関数にそれぞれの規格化因子を掛けたもので行うことになりますが、これらの係数は一つの係数として括られ、G関数に含めることができますから、結果は同じになります。
さて、3d軌道は4周期のスカンジウム以降に現われます。
最外殻にd電子があり、この軌道とこの上位のs軌道(d電子より一つ上のエネルギー順位のものですが、d電子が入っていない場合には、こちらの方がエネルギー順位が低くなります)が満たされていない元素は遷移金属と呼ばれ、d電子は主に錯体の形成や金属結合と関係することになります。
7. 原子における電子配置
原子の中の各電子は、エネルギーの低い順位の軌道から詰まっていくことになります。
ただし、各軌道にはパウリの排他原理により電子は2つまでしか入ることができません。
また、電子同士は反発しあうことより、同一のエネルギー順位の軌道がある場合、空いているところに入ることになる。
同順位の軌道全てに電子が詰まった場合には、対になって入っていくことになります。
ただし、エネルギー順位が高くなり、他軌道とのエネルギー差が小さくなった場合には、同軌道が全て詰まる前に他軌道に入る場合があります。
また、方向性が特に強くなるf軌道の場合には、この軌道をスキップして、この上位のs軌道などから詰まることもあります。
電子のエネルギーは、水素原子の場合では電子が一つしかないため、主量子数が同じであれば、同一のエネルギーとなります。
しかし、多電子となる水素以外では主量子数が同じでもエネルギーが同じになるとは限りません。
この理由は、電子が詰まっていくことにより核電荷の遮蔽効果が生じること、軌道関数での電荷の分布が異なることによります。
一般的傾向としては、主量子数が同じ場合、方位量子数が大きくなるほど電子のエネルギーが高くなります。
各元素の電子配置については、「元素の電子配置」を参照して下さい。
電子殻
これは主量子数が同じ電子によって充填されたものとなります。
この殻は、K殻、L殻、M殻、N殻と呼ばれ、次のようになります。
| 電子殻 | 充填電子 | 備考 |
|---|
| K殻 | 1s電子 | 第1周期 |
| L殻 | 2s電子,2p電子 | 第2周期 |
| M殻 | 3s電子,3p電子,3d電子 | 第3周期には3d電子は含まれない。 |
| N殻 | 4s電子,4p電子,4d電子,4f電子 | 第4周期には3d電子が含まれ、4d・4f電子は含まれない。 |
第4周期は3d電子ではなく、4s電子から始まりますが、これは3d電子よりも4s電子の方がエネルギー順位が低いためです。
このことは、次のように考えることができます。
3p電子が充填した場合、ほぼ球状の亜殻ができますから、電荷雲の分布が偏った3d電子よりは、この分布が球状の4s電子の方が電子同士の反発力が弱くなると考えることができます。
また、主量子数が3dくらいになると、次のエネルギー順位との差がかなり小さくなることも関係しています。
L殻については、2s電子と2p電子とのエネルギー差が大きいことから、2s軌道も亜殻と考えることができます。
なお、2p電子は主量子数が2からとなり、3d電子はこれが3からとなります。
また、4f電子はこれが4からとなります。
パウリの排他原理というのは、ある配置(原子内など)において同一の量子状態をもつ電子は2つ以上存在することができない、というものです。
この量子状態というのは4つの量子数のことで、これは主量子数、方位量子数、磁気量子数、スピン量子数です。
軌道は主量子数、方位量子数、磁気量子数の3つによって定まるため、同一軌道にはスピンが異なるものだけが入ることができますが、スピンは-1/2または1/2の値しかとることができないため、同一軌道には電子は2つまでしか入ることができません。
この排他原理は、電子のように半整数スピンをもつフェルミ粒子に対してとなります。
一方、光子はスピン1を持ち、このように整数スピンを持つものはボーズ粒子と呼ばれ、これには適用されません。
8. 混成軌道
原子の基底状態では、電子配置は、1s軌道、2s軌道、2p軌道とエネルギーが低い順位のものから詰まっていきますが、原子同士が共有結合をすることによってエネルギーが与えられると、2s軌道から2p軌道というように昇位することが可能となります。
特に炭素原子やホウ素では2p軌道が空いているため、この軌道に昇位しやすくなっています。
これらの原子の2s電子が2p軌道に移ることにより、2s軌道は対電子の状態から不対電子1個の状態となります。
そこで、炭素の場合について示すと次のようになります。
| 状態 | 1s | 2s | 2p |
|---|
| 励起前 | ‥ | ‥ | ・ | ・ | |
| 励起後 | ‥ | ・ | ・ | ・ | ・ |
この結果、不対電子は4個となり、炭素の共有原子価が4となることが説明できます。
ただし、不対電子の2s電子と2p電子とは重なりが生じ、これらの軌道を合成した混成軌道を考えることになります。
この混成軌道としては、sp混成軌道、sp2混成軌道、sp3混成軌道があります。
sp混成軌道 2s電子1個と2p電子1個を重ね合わせたものです。
この混成軌道についていう前に、電子軌道を個別に取り扱うにはそれぞれは直交性を持たなければならないことです。
直交性とは、ベクトルでいえば二つのベクトルが直交していることですが、このことはこれらの内積が0になることを意味しています。
これと同じように、波動の場合には直交性を次のように定義します。
二つの波動関数をψ1,ψ2とすると、これらが直交しているとは次の式が成立することです。
ここで、dτは体積要素のことで、積分は全空間について行います。
例えば、1s軌道と2p軌道とは直交していて、これは次のように示すことできます。
| ò |
N1sexp(-ra)・N2pxexp(-ra/2)dt |
=N1s・N2p |
ò |
xexp(-3ra/2)dt |
| |
ここで、exp(-3ra/2)は球対称な関数で、xはx軸について反対称な関数(つまり、¦(-x)=-¦(x)となること)ですから、これらの積はx軸について反対称となることから、この積分は0となります。
このように、各原子軌道は直交性を持っています。
このため、これらの一次結合から作られる波動関数は、これらの直交性を用いることになり、8.1式を直接的に証明するということはありません。
また、幾つかの原子軌道から作った波動関数は、これら同士で直交することを示せば、他の原子軌道に対して直交性を示す必要はありません。
例えば、ψaとψbから作った次の一次結合
は、他の原子軌道ψcとは、次のように直交することになります。
| ò |
φ・ψcdt |
= |
ò |
aψaψcdt |
+ |
ò |
bψbψcdt |
=0 |
| |
さて、sp混成軌道は、s電子1個とp電子1個から作ることより、これらの混成軌道は2個できる必要があります。
これらの混成軌道は、次のものになります。
ここで、sは2s軌道、pは2p軌道となります。
これらの直交性は、次のように示すことができます。
| ò |
ψ1ψ2dt |
= |
ò |
(s+p)(s-p)dt |
= |
ò |
s2dt |
- |
ò |
p2dt |
=1-1=0 |
| |
8.2a式は、x軸上では次のような関数となります。
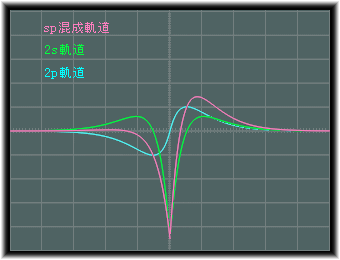
ここで、2s軌道は6.2b式のものとなっています。
一方、8.2b式の方はこの正側と負側を入れ換えたものとなります。
イメージ的には、8.2a式は次のようになります。
(ただし、係数 1/√2を掛けて正規化したものとなります。)
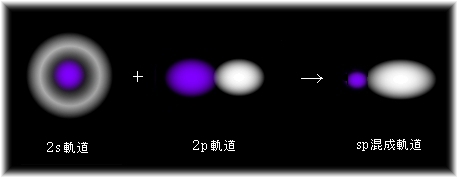
2p軌道に2s軌道を重ねたものは、2s軌道が球対称であることから、この外側の部分では同相側の値を大きくし、逆相側の値は小さくします。
したがって、このことは2p軌道の2方向性を1方向性のものにするということになります。
そのように、φの向きを考えるにはp軌道だけを考えればよいことになります。
なお、この原点である原子核付近では、電子が存在しても、他の原子の電子と重なり合うことはないのですから、この部分は無視できます。
8.2b式(を正規化したもの)の方は次のようになります。
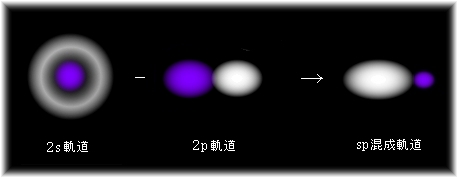
sp混成軌道は不対2p電子が2個余っていることから、sp混成軌道とこれらの不対電子によって、それぞれ二重結合を作ることができます。
これとしては、二酸化炭素(O=C=O)があります。
sp2混成軌道は2s電子1個と2p電子2個の混成軌道です。
これは、三つのsp混成軌道様の電子からなる、三方平面形のものとなります。
この混成軌道は、次のように表すことができます。
ここで、a, b, cはある係数です。
これを考える前に、pxとpyとの重ね合わせがどのようになるかということを説明します。
まず、p軌道を一つのベクトルと考えると、pxとpyとの一次結合は次の図のようになるとされます。
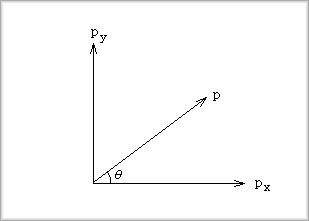
式で表すと、次のようなります。
p=pxcosq+pycos(p/2-q)=pxcosq+pysinq
| (8.4) |
cosθは、ベクトルの場合と同様に、pとpxの「内積」(重なり積分のこと)を取ることによって得られます。
つまり、これは次のようになります。
| ò |
px(pxcosq+pysinq)dt |
= |
ò |
px2cosqdt |
+ |
ò |
pxpysinqdt |
=cosq |
| |
このようなことは、8.4式の任意のp同士でも成立します。
つまり、次の式が成立します。
ここで、θはp1とp2との間の角度です。
上式を証明するために、まずp1,p2を次のようにおきます。
これらの積を積分すると次のようになります。
|
|
| = |
ò |
(pxcosa+pysina)(pxcosb+pysinb)dt |
|
|
| = |
ò |
px2cosacosbdt |
+ |
ò |
py2sinasinbdt |
|
|
| =cosacosb+sinasinb=cos(a-b)=cosq |
|
| |
したがって、8.3式は次のように表すことができます。
ここで、pはxy平面においてある角を向いたp軌道です。
また、s軌道は三つのものと分けて用いることから、この係数λは1未満の数となります。
したがって、これはsp混成軌道様のものと考えることができます。
三方向のp軌道を等間隔でおくという場合には、これらの間の角度は120゜となり、これがsp2混成軌道ということになります。
さて、λの値ですが、これは各混成軌道同士が直交するという条件から得られ、これは1/√2になります。
ψ1,ψ2をsp2混成軌道の任意の二つの軌道として、これらの重なり積分は次のようになります。
|
|
|
|
| = |
ò |
p1p2dt |
+ |
ò |
lp1sdt |
+ |
ò |
lp2sdt |
+ |
ò |
l2s2dt |
|
|
|
| |
これらが直交することより、この積分は0となりますから、次のようにλが定まります。
| cosq+l2=cos120゚+l2=0 ∴ l= |
Ö |
____
0.5
|
| |
sp混成軌道の場合とでは、s軌道の混成比率が異なるものとなりますが、s軌道の小さいものを掛けることは、sp混成軌道の広がりが小さくなる、ということを意味します。
このことは共有結合での重なりが小さくなることから、sp混成軌道のものよりも、結合が少し弱くなります。
なお、sp2混成軌道は不対2p電子が1個余ることから、sp2混成軌道とこの不対電子によって、一つの二重結合を作ることができます。
このように結合した例としては、炭素6員環によるベンゼン環があります。
これは60゜ずつ曲がっていくことから、6個でちょうど一回りする環となります。
sp3混成軌道は2s電子1個と2p電子3個の混成軌道です。
これは四つのsp混成軌道様の電子からなり、これらの各端点は四面体構造を形成します。
というのは、それが空間上で4つのものが最も対称的になる配置だからです。
炭素原子ではこれが、二重結合がない場合の基本的な電子配置となります。
この混成軌道は、次のように表すことができます。
ここで、a,b,c,dはある係数です。
この場合も、sp2軌道と同じように、各p軌道を重ね合わせたものを考えます。
これは、xy平面上のp軌道とpzとの重ね合わせになりますから、次のようなp'軌道になります。
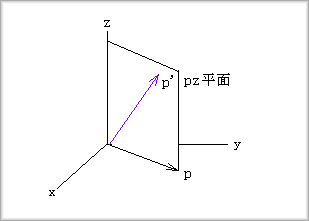
このような軌道が4つあるということになりますから、これらの配置方向は四面体の各頂点方向となります。
そこで、四面体の各頂点がどのようになるかですが、これは立方体の各頂点に次のように置いたものとなります。
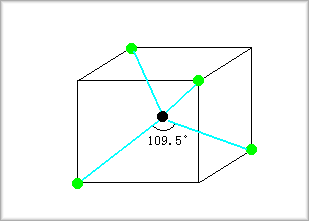
上記混成軌道が成す角θは109.5°となりますが、これは次の図より求めることができます。
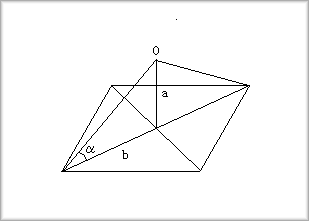
立方体の一辺の長さを1とすると、aの長さは 1/2となり、bの長さは √2/2となります。
これより、角αは次のようになります。
a=tan-1(a/b)=tan-1(1/√2)≒35.264°
| |
したがって、結合角θは次のようになります。
q=180゚-2a≒109.47゚=109゚28'
| |
sp3混成軌道の場合には、s軌道を四つに配分するということになり、この場合の8.6式のλは次のようになります。
l2=-cosq=-cos(109.47…゚)=0.3333…=1/3
| |
なお、結合の強さは、計算および実験から、次のようになるとされます。
このことは、次のように考えることができます。
共有結合の強さは、重なりが大きいほど強くなります。
σ結合の場合では、方向性が強く、しかも端部分が膨らんでいるものが強いということになります。
したがって、この順序はまずsp等の混成軌道、p軌道、s軌道の順となります。
この混成軌道の中でも、p軌道性の強いものがより外側に膨らむことになります。
このことは8.6式のλの値を比較すればよく、これはsp,sp2,sp3の順となります。
窒素
炭素の場合と同じように、窒素の場合も混成軌道を形成するのではないかと考えるかもしれませんが、実際そのようになっています。
というのは、アンモニア(NH3)の場合、各水素との結合角は107゜で、これは四面体の場合の角度109゜に近くなっているからです。
この場合には、4つあるsp3混成軌道の一つには非共有結合電子対が入ります。
これは次の図のようになります。
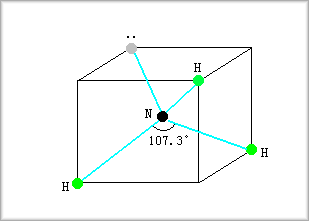
非共有電子対がある部分は電子密度が高いため陽イオンの水素を引きつけることができ、窒素は塩基性を示します。
なお、窒素の場合に混成軌道のことがあまり言われないのは、別に混成軌道を考えなくてもよいからと考えられます。
つまり、窒素の結合原子価は3価ですが、これは不対電子3個で考えることができるからです。
酸素
酸素も場合もsp3混成軌道を形成すると考えられます。
例えば、水分子の場合、水素との結合角は104.5゜となっていて、これは明らかに不対2p電子2個で共有結合を作るとした場合の90゜よりは、四面体の場合の結合角109.5゜に近くなっています。
酸素の場合には、M殻には2s電子は2個で、2p電子が4個ありますから、これらを4つのsp3混成軌道に配置するとした場合には、2つには非共有電子対が入り、残りの2つには電子が1個ずつ入ると考えることができます。
(ただし正確なものではありませんが。)
つまり、酸素の電子配置は次のように変わったと考えることができます。
| 状態 | 1s | 2s | 2p |
|---|
| 励起前 | ‥ | ‥ | ‥ | ・ | ・ |
| 1s | sp3 |
|---|
| 励起後 | ‥ | ‥ | ‥ | ・ | ・ |
波動の場合には、特に明確な形があるわけではなく、これは様々に変わることができます。
このことは風船の場合と同じです。
風船は外から加えられた力によって様々に変形することになります。
特に物質波の場合には、これは仮想的なものであり、実在しているものではありません。
(この「実在性」は、電子の存在確率分布を調べることによって現れるのみです。)
このことは、如何なる物理的制約もないということを意味しています。
これを規定するものは、単に定常波を形成することができるか、また最もエネルギー状態が低く、安定になり得るか、ということなどとなります。
さて、混成軌道といったものが本当に存在するものなのかということが疑問になりますが、そもそもs電子やp電子といったものは、シュレーディンガーの波動方程式を解いて得られたものにすぎず、そのような電子というのは条件が変われば変わることになります。
ただ、波動はそうした基本的な波動の重ね合わせによって表現できるために、それらの軌道が基本的なものとみなされているにすぎません。
一般的には、エネルギー状態に応じて適切な直交的波動関数の組ができ、これを基本的な波動関数とすることができます。
そこで、励起後のsp3混成軌道の不対電子がそれぞれ水素と共有結合をすることになります。
これは、次の図のようになります。
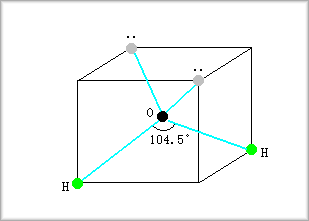
炭素の場合と違って、水素との結合角が少し小さくなるのは、(他方に原子核がない)非共有結合電子対同士の反発が、共有結合電子対よりも強いためと考えることができます。
なお、酸素の非共有電子対と水素とは水素結合が生じることから、酸素によって四面体が形成されます。
酸素の場合にも、上側の電子密度が高いことから、水素イオンを引きつけることができるため、塩基性を示すことになります。
リン
リンは窒素と同じくⅤⅢ属の元素で窒素と似た電子配置となりますが、最外殻の電子の主量子数は3である点が大きく異なります。
つまり、M殻の元素の場合には3p軌道の次のエネルギー順位である3d軌道があり、これへの遷移が可能になります。
したがって、リンの場合にはd軌道も含めた混成軌道やこれとの結合性が生じます。
リンの主な励起状態を示すと以下のようになります。
| 状態 | 3s | 3p | 3d |
|---|
| 励起前 | ‥ | ・ | ・ | ・ | | | | | |
| sp3 | 3d |
|---|
| 励起後(1) | ‥ | ・ | ・ | ・ | | | | | |
| 励起後(2) | ・ | ・ | ・ | ・ | ・ | | | | |
| sp3d | 3d |
|---|
| 励起後(3) | ‥ | ・ | ・ | ・ | | | | | |
| 励起後(4) | ・ | ・ | ・ | ・ | ・ | | | | |
sp3d混成軌道の各頂点(電荷雲の張出し)による形は、正四面体を二つ貼り合わせた三方両錐形になり、これらはσ結合をします。
また、d軌道はこのσ結合に対してπ結合をすることになります。
したがって、この場合には、X3P=Yという形の化合物を作ることになります。
単体のリンとしては白色リン(黄リン)、赤色リン、黒色リンがあります。
白色リンはP4単位のものがファンデルワールス力で緩く結合しているもので、これは反応性が高く毒性などを示すので注意が必要です。
例えば、白リンが皮膚につくと傷害を起したり、白リンを空気中に放置すると50℃以上で発火します。
また、白リンの致死量は0.15gと猛毒であるため、誤って食品に混ぜたりしないように注意する必要があります。
イオウ
イオウは酸素と同じくⅤⅣ属の元素で酸素と似た電子配置となりますが、これはリンの場合よりも複雑な状態が生じます。
この主な励起状態を示すと以下のようになります。
| 状態 | 3s | 3p | 3d |
|---|
| 励起前 | ‥ | ‥ | ・ | ・ | | | | | |
| sp2 | 3p | 3d |
|---|
| 励起後(1) | ‥ | ・ | ・ | ・ | ・ | | | | |
| 励起後(2) | ・ | ・ | ・ | ・ | ・ | ・ | | | |
| sp3 | 3d |
|---|
| 励起後(3) | ‥ | ‥ | ・ | ・ | | | | | |
| 励起後(4) | ‥ | ・ | ・ | ・ | ・ | | | | |
| 励起後(5) | ・ | ・ | ・ | ・ | ・ | ・ | | | |
| sp3d | 3d |
|---|
| 励起後(6) | ‥ | ・ | ・ | ・ | ・ | | | | |
| 励起後(7) | ・ | ・ | ・ | ・ | ・ | ・ | | | |
| sp3d2 | 3d |
|---|
| 励起後(8) | ・ | ・ | ・ | ・ | ・ | ・ | | | |
sp3d2混成軌道の各頂点(電荷雲の張出し)による形は、正八面体になります。
励起後(1)では、2つのσ結合に対してそれぞれπ結合が生じることから、X=S=Y型の化合物(SO2など)を作ります。
励起後(2)では、3つのσ結合に対してそれぞれπ結合が生じることから、3個の原子と3方向に二重結合した化合物(SO3など)を作ります。
励起後(3)では、2つのσ結合が生じ、これは2価での化合物(H2S,SCl2など)によく見られるものです。
励起後(4)では、3つのσ結合に対して、1つのπ結合が生じることから、X2S=Y型の化合物(SOCl2など)を作ります。
励起後(5)では、4つのσ結合に対して、2つのπ結合が生じることから、X2S(=Y)2型の化合物(SO2(OH)2=H2SO4など)を作ります。
なお、硫酸は励起による混成軌道を考えないで、酸素とは配位結合(非共有電子対の供与と受容によるもの)するという見方もあります。
この場合には、酸素とは配位結合による単結合となります。
励起後(6)では、歪んだ四面体型となり、4個の原子と単結合を行ないます。
励起後(7)では、三方両錐形となり、5つのσ結合に対して、1つのπ結合が生じることから、X4S=Y型の化合物(SOF4など)を作ります。
励起後(8)では、正八面体となり、6つのσ結合が生じることから、SX6型の化合物(SF6など)を作ります。
【補遺】
- 原子量と分子量
-
原子量とは質量数12の炭素の質量(この規定は1961年になされました)の1/12の値を単位にした、原子の相対質量のことです。
ただし、同一の原子でも同位体のものがありますから、それぞれ存在比を掛けて平均したものになります。
また、分子量は分子に含まれている各原子の原子量の総和をとったものになります。
ところで、原子の質量はほとんど原子核の重さになります。
また、原子核は質量がほとんど同じになる陽子と中性子からなります。
原子核が安定するのは、塩素までは、陽子と中性子の数が同数か、中性子の方が一個多い場合となります。
なお、その場合、陽子数が偶数では同数となるものが多く(例外はベリリウムになります)、奇数では中性子の方が一個多いものがほとんどです(例外は窒素になります)。
したがって、上記のことと分子に含まれる元素のほとんどは塩素までの元素となることから、分子量は分子に含まれる陽子数の約2倍になり、これは分子内の電子数の約2倍ということになります。
- 波数
-
振動数というのは1秒間当たりの横波の振動の回数のことであり、また波が1秒間に進む長さは波の速度vですから、vの距離の間にν個分の振動が含まれることになります。
単位長当りでは、ν/v個の波の数があることになって、これは波数と呼ばれます。
電磁波では、これはν/c個になります。
また、波の速度vは単位時間当りの1回の振動の長さである波長λより、v=λνとなりますから、波数ν'は
となって、波数は波長の逆数になります。
(なお、2πを単位長とする場合もあり、この場合の波数は2π/λとなります。
2πは1単位長の円周となりますから、この場合の波数は1秒間に進む波の位相に関係したものとなって、これは角波数とも呼ばれます。)
そこで、振動数νの代りに波数ν'を用いて、軌道遷移による電子の放出エネルギーとの関係を表わすと
| n'=n/c = |
hn
──
hc |
= |
E
──
hc |
= |
me4Z2
─────
8e02h3c |
・ |
( |
1
───
n12 |
- |
1
───
n22 |
) |
=RZ2 |
( |
1
───
n12 |
- |
1
───
n22 |
) |
| |
となります(MKSA系の場合)。
エネルギーEは5.9式によります。
上式で、煩瑣な係数をまとめた Rはリュードベリ定数(カナ名は様々となります)と呼ばれるもので、これは次の値になります。
|
R=1.0973731×107[m-1]=1.0973731×105[cm-1]
| |
電磁波の場合にはMKSA単位系ではなくCGS単位系を使うことが多く、この場合の波数とは1cm当りの波の数を言います。
なお、振動数ではなく波数を用いるのは、可視光付近の振動数が非常に高いことから記載に不便なためで、原子スペクトルなどを研究する分光学では波数を用いています。
もっとも、原子の半径の大きさ程度である10-8cmを表わすÅ(オングストローム)を用いて波長を表わせば、そうした記載の不便はなくなりますが、これでは振動数と逆比例の関係となり、あまり良くありません。
- 電子の呼び名
-
分光学ではエネルギー順位を方位量子数によって列毎に分けて表わしていて、各列の系列のエネルギー順位は、l=0,1,2,3に対応して、S,P,D,F順位と名づけられました。
S,P,D,Fの記号の意味は、sharp series(鋭系列)、principle series(主系列)、diffuse series(鈍系列)、fundamental series(基本系列)となっています。
原子の状態は、これから放出される電磁波のスペクトルを調べることによって行われたことから、電子状態はそうした分光学の用語と関係づけられました。
- ドップラー効果
-
ドップラー効果というのは、波を発する物体と観測者との相対速度の変化によって生じる振動数の変化をいうものです。
これには音のドップラー効果と光のドップラー効果がありますが、両者は同じ波動でも根本的二個となります。
つまり、音の場合の波動は空気という物質の運動によって生じているのですが、光の場合には光子という、どちらかと言えば非物質的なもの(純粋な波動という意味ですが)の運動によって生じています。
物質の場合には、粒子の運動ですから、観測系の速度が変化すれば、その速度は変化することになります。
このため、縦波である音の波動は、観測者に対して進む場合には振動数が高くなりますが、観測者から離れていく場合には振動数が低くなります。
このことは、救急車のサイレンの音など日常的によく経験することです。
一方、光の場合には光速度が一定となることから、観測者の相対速度の変化に対して不変となります。
しかし、光源と観測者との距離は観測者の運動によって変化することになるのですから、この差分を相殺する必要があります。
これは光の振動数の変化によって補われることになります。
つまり、光が進む距離は、波長×振動数となります。
…
これにより光源との相対速度が大きくなる場合には振動数が高くなり、相対速度が小さくなる場合には低くなります。
粒子の運動の場合、相対速度の変化は運動エネルギーの変化となるように、光子の場合でも光源との相対速度の変化は、光子の振動数の変化によるエネルギーの変化(E=hν)となって現れます。
参考文献
| 番号 | 書名 | 著者 | 訳者 | 出版社 |
|---|
| 1 | 原子スペクトルと原子構造 | G.Herzberg | 堀健夫 | 丸善 |
| 2 | 初等量子力学 | W.ハイトラー | 久保昌二・木下達彦 | 共立全書 |
| 3 | 分子の形と構造 | C.A.Coulson, R.McWeeny | 千葉秀昭・阿竹徹 | 東京化学同人 |
| 4 | 量子力学Ⅰ | 朝永振一郎 | | みすず書房 |
| 5 | 量子化学 1 | P.W.アトキンス | 土方克法 | みすず書房 |
| 6 | 原子価と分子構造(4版) | E.Cartmell and G.W.A.Fowles | 久保昌二 | 丸善 |
| 7 | クールソン 化学結合論 第2版 | C.A.Couslon | 関集三・千原秀明・鈴木啓介 | 岩波書店 |
| 8 | 量子論にパラドックスはない | P.R.Wallace | 荒巻正也・粟屋かよ子・沢田昭二 | シュプリンガー・フェアラーク東京 |















